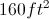We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Trapezoids

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Perimeter Of A Trapezoid

Find the perimeter of the trapezoid below.

Possible Answers:

234

300

210

214

200

Correct answer:

200

Explanation:

We can then use the Pythagorean Theorem to find the right portion of the bottom base. We can then use this value to determine the left portion.

Using Pythagorean Theorem again, we can calculate the left leg to be 20. That means we now know all four sides. The perimeter is simply the sum.

$\small P=20+52+34+94=200$

Report an Error

Example Question #1 : How To Find The Perimeter Of A Trapezoid

An isosceles trapezoid has two bases that are parallel to each other. The larger base is times greater than the smaller base. The smaller base has a length of 2.5 inches and the length of non-parallel sides of the trapezoid have a length of 4.5 inches.

What is the perimeter of the trapezoid?

Possible Answers:

23in

21.5in

11.5in

10.5in

23.5in

Correct answer:

21.5in

Explanation:

To find the perimeter of this trapezoid, first find the length of the larger base. Then, find the sum of all of the sides. It's important to note that since this is an isosceles trapezoid, both of the non-parallel sides will have the same length.

The solution is:

The smaller base is equal to 2.5 inches. Thus, the larger base is equal to:

$2.5\times4=10$

Perimeter=base1+base2+(2S) , where the length of one of the non-parallel sides of the isosceles trapezoid.

$P=2.5+10+(2\times 4.5)$

P=2.5+10+9=21.5

Report an Error

Example Question #1 : How To Find The Perimeter Of A Trapezoid

Dr. Robinson's property is shaped like an isosceles trapezoid. Dr. Robinson gave a contractor the following measurements, so that the contractor can build a wall around the enire property.

Measurements of property:

base1: 15 yds

base2:7.5yds

non-parallel-sides: 8yds

Find the perimeter of Dr. Robinson's property.

Possible Answers:

30.5

42yds

28.5yds

38.5yds

28yds

Correct answer:

38.5yds

Explanation:

The measurements that Dr. Robinson gave to the contractor include the lengths of the two base sides and one of the non-parallel sides of the property. Since Dr. Robinson's property is shaped like an isosceles trapezoid, there must be two non-parallel sides of equal length.

The solution is:

P=15+7.5+2(8)=15+7.5+16=38.5

Report an Error

Example Question #291 : Intermediate Geometry

Find the area of the following trapezoid.

Geo_area2

Possible Answers:

$160 ft^{2}$

$128 ft^{2}$

$152 ft^{2}$

$96 ft^{2}$

$190 ft^{2}$

Correct answer:

$128 ft^{2}$

Explanation:

The correct answer is 128 sq ft.

There are two ways to find the total area. One way to find the total area, you must find the area of the triangle and rectangle separately. After some deduction (19ft -13ft) , you can find that the base of the triangle is 6 ft. Then using the Pythagorean Theorem, or 3-4-5 right triangles, you can find that the height of the triangle and rectangle is 8 ft. Geo_area2b

To find the area of the triangle, you would multiply 6 by 8 and then divide by 2 to get 24. To find the area of the rectangle, you would multiply 8 by 13 to get 104. Then you would add both areas to get 128 sq ft.

Geo_area2c

The other way to find the area is to use the formula for area of a trapezoid. After some deduction (19ft -13ft) , you can find that the base of the triangle is 6ft. Then using the Pythagorean Theorem or 3-4-5 right triangles, you can find that the height of the triangle and rectangle is 8 ft.

Then you use the formula:

${\frac{1}{2}}h (b_{1} +b_{2})$

to get

$\frac{1}{2}\cdot 8(13+19)=128sq ft$

Report an Error

Example Question #31 : Trapezoids

Find the length of if the area of the trapezoid below is 320 .

Possible Answers:

Cannot be determined from the information given.

Correct answer:

Explanation:

Start by drawing in the height, , to form a right triangle.

Use the Pythagorean Theorem to find the length of .

24^2+(CE)^2=26^2

576+(CE)^2=676

(CE)^2=100

CE=10

Now that we have the height, plug in the given information into the formula to find the area of the trapezoid.

Keep in mind that AE+ED=AD .

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$

$320=\frac{1}{2}(14+AE+24)(10)$

$\frac{1}{2}(AE+38)=32$

AE+38=64

AE=26

The question asks you to find the length of .

AD=AE+ED

AD=26+24=50

Report an Error

Example Question #33 : Trapezoids

Find the length of . The area of the trapezoid is . Round to the nearest hundredths place.

Possible Answers:

11.77

10.45

8.94

9.02

Correct answer:

9.02

Explanation:

First, draw in the height .

First, find by using $\text{sine}$ .

$\sin 53=\frac{CE}{10}$

$CE=10\sin 53=7.99$

Now, plug in the values for area, height, and one base to find the length of the second base, .

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$

$60=\frac{1}{2}(6+AD)(7.99)$

$\frac{1}{2}(6+AD)=7.51$

6+AD=15.02

AD=9.02

Report an Error

Example Question #34 : Trapezoids

Find the length of . The area of the trapezoid is 106 . Round to the nearest hundreths place.

Possible Answers:

6.01

10.00

12.04

8.06

Correct answer:

8.06

Explanation:

First, draw in the height.

First, find the height by using $\text{sine}$ .

$\sin 78=\frac{height}{12}$

$height=12 \sin 78=11.74$

Now, plug in the values for area, height, and one base to find the length of the second base, .

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$

$106=\frac{1}{2}(10+AD)(11.74)$

$\frac{1}{2}(10+AD)=9.03$

10+AD=18.06

AD=8.06

Report an Error

Example Question #32 : Trapezoids

Find the length of . The area of the trapezoid is 500 . Round to the nearest hundredths place.

Possible Answers:

47.85

49.00

46.29

53.00

Correct answer:

49.00

Explanation:

First, draw in the height.

First, find the height by using $\text{sine}$ .

$\sin 66=\frac{height}{15}$

$height=15\sin 66=13.70$

Now, plug in the values for area, height, and one base to find the length of the second base, .

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$

$500=\frac{1}{2}(24+AD)(13.70)$

$\frac{1}{2}(24+AD)=36.50$

24+AD=73.00

AD=49.00

Report an Error

Example Question #36 : Trapezoids

Find the value of if the area of this trapezoid is .

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a trapezoid is

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$ .

Substitute in the values for the area, a base, and the height. Then solve for .

$90=\frac{1}{2}(14+a)6$

180=(14+a)6

14+a=30

a=16

Report an Error

Example Question #31 : Trapezoids

Find the value of if the area of this trapezoid is 130 .

Possible Answers:

Correct answer:

Explanation:

The formula to find the area of a trapezoid is

$\text{Area}=\frac{1}{2}(base_1+base_2)(height)$ .

Substitute in the values for the area, a base, and the height. Then solve for .

$130=\frac{1}{2}(17+b)5$

260=(17+b)5

17+b=52

b=35

Report an Error

View Tutors

Joshua
Certified Tutor

Murray State University, Bachelor in Arts, Spanish. Lipscomb University, Bachelor of Science, Teacher Assistant.

View Tutors

Kaylee
Certified Tutor

Brigham Young University, Bachelor, MFA - Animation.

View Tutors

Lydia
Certified Tutor

The Richard Stockton College of New Jersey, Bachelor of Science, Biochemistry and Molecular Biology.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Los Angeles, Physics Tutors in Philadelphia, Physics Tutors in San Diego, Biology Tutors in Phoenix, MCAT Tutors in Denver, SSAT Tutors in Seattle, SAT Tutors in Boston, GRE Tutors in Denver, SSAT Tutors in Denver, English Tutors in San Diego

Popular Courses & Classes

GMAT Courses & Classes in Miami, GRE Courses & Classes in San Diego, MCAT Courses & Classes in Boston, LSAT Courses & Classes in Seattle, GRE Courses & Classes in Boston, MCAT Courses & Classes in Seattle, ISEE Courses & Classes in Boston, ISEE Courses & Classes in New York City, SAT Courses & Classes in Miami, LSAT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in New York City, ACT Test Prep in Los Angeles, GRE Test Prep in Boston, GRE Test Prep in Chicago, GRE Test Prep in San Diego, LSAT Test Prep in Atlanta, GRE Test Prep in Dallas Fort Worth, ACT Test Prep in Dallas Fort Worth, SSAT Test Prep in Denver, GMAT Test Prep in Philadelphia

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Trapezoids

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #1 : How To Find The Perimeter Of A Trapezoid

Example Question #1 : How To Find The Perimeter Of A Trapezoid

Example Question #1 : How To Find The Perimeter Of A Trapezoid

Example Question #291 : Intermediate Geometry

Example Question #31 : Trapezoids

Example Question #33 : Trapezoids

Example Question #34 : Trapezoids

Example Question #32 : Trapezoids

Example Question #36 : Trapezoids

Example Question #31 : Trapezoids

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: