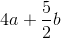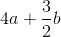All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Length Of The Side Of A Hexagon
An apothem is a line drawn from the center of a regular shape to the center of one of its edges. The line drawn is perpendicular to the edge. A regular hexagon has an apothem of 
Cannot be determined
If the apothem is 
As long as one angle and one side length is known for a right triangle, trig functions can be used to solve for a mystery side. In the previous image, the side of interest has been labeled as 





This measure of 

Now that we have the apothem and one of the angles, we can use trig functions to solve for 
Using SOH CAH TOA, we realize that this problem would require us to use the tan function where the ratio would be 

Now 


Example Question #2 : How To Find The Length Of The Side Of A Hexagon
Suppose the perimeter of a hexagon is 
Write the perimeter formula for hexagons.
Substitute the perimeter in the formula and solve for the side length.
Example Question #3 : How To Find The Length Of The Side Of A Hexagon
Let the perimeter of a hexagon be 
Write the formula for finding the perimeter of a hexagon.
Substitute the perimeter and solve for the side length.
Example Question #4 : How To Find The Length Of The Side Of A Hexagon
If the perimeter of a hexagon is 
Write the perimeter formula for a hexagon.
Substitute the perimeter into the formula and solve for the side length.
Example Question #1 : How To Find The Length Of The Side Of A Hexagon
If the perimeter of a regular hexagon is 
Write the formula for the perimeter of a hexagon.
Substitute the perimeter and solve for the side.
Example Question #6 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #7 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #8 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #9 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #10 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Certified Tutor
All Intermediate Geometry Resources