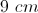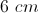All Intermediate Geometry Resources
Example Questions
Example Question #2 : How To Find If Parallelograms Are Similar
A parallelogram has adjacent sides with the lengths of 

Since the two parallelogram are similar, each of the corresponding sides must have the same ratio.
The ratio of the first parallelogram is:
Applying this ratio we are able to find the lengths of the second parallelogram.
Example Question #271 : Quadrilaterals
A parallelogram has adjacent sides with the lengths of 

Since the two parallelogram are similar, each of the corresponding sides must have the same ratio.
The ratio of the first parallelogram is:
Thus by simplifying the ratio we can see the lengths of the similar triangle.
Example Question #1 : Acute / Obtuse Isosceles Triangles
An isosceles triangle has a base of 


Example Question #1 : Triangles
An isosceles triangle has a perimeter of 
The height of the triangle cannot be determined with the given information.
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #2 : Triangles
An isosceles triangle has a perimeter of 

First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #3 : Triangles
An isosceles triangle has a perimeter of 
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #4 : Triangles
An isosceles triangle has a perimeter of 
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #5 : Triangles
An isosceles triangle has a perimeter of 
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #6 : Triangles
An isosceles triangle has a perimeter of 
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Example Question #7 : Triangles
An isosceles triangle has a perimeter of 
First, find the lengths of the triangle.
Let 

Use the information given about the perimeter to solve for 
Plug this value in to find the length of the base.
Now, recall that the height of an isosceles triangle can split the entire triangle into two congruent right triangle as shown by the figure below.

Thus, we can use the Pythagorean Theorem to find the length of the height.
Plug in the given values to find the height of the triangle.
Make sure to round to 
Certified Tutor
All Intermediate Geometry Resources