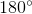All Intermediate Geometry Resources
Example Questions
Example Question #11 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #12 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #13 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #14 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #15 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #16 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #17 : How To Find The Length Of The Side Of A Hexagon
Find the length of a side of a regular hexagon that has its center at 

This is a regular hexagon; therefore, when we draw in the diagonals, we will create 

Now, the given line segment also serves as the height to the newly created equilateral triangles. This height also splits an equilateral triangle into two congruent 
Recall that 

Substitute in the given height into the ratio in order to find the length of the base of the 
Substitute.
Solve.
The length of the side of the hexagon is twice the length of the base.
Substitute in the value of the length of the base to find the side length of the hexagon.
Solve.
Example Question #11 : How To Find The Length Of The Side Of A Hexagon
Given: Regular Hexagon 




True or false: Quadrilateral 
True
False
True
Below is regular Hexagon 



Each angle of a regular hexagon measures 

Also, each central angle is one sixth of a complete circle, so 
This makes 

and
By transitivity,

Quadrilateral 
Example Question #11 : How To Find The Length Of The Side Of A Hexagon
Five sides of a hexagon are known to have length 10; the perimeter of the pentagon is 60.
True, false, or undetermined: The hexagon is regular.
False
Undetermined
True
Undetermined
If the hexagon has perimeter 60, and five of its sides are known to have length 10, then the length of its sixth side is

All six sides are of the same length, so the hexagon is equilateral. However, for the hexagon to be regular, it must hold that all six angles are of the same measure as well - that is, it must also be equiangular. However, an equilateral hexagon may or may not be equiangular, as seen by the figures below; both are equilateral hexagons, but only the left one is equiangular.

Therefore, the question of whether the hexagon is regular cannot be answered without further information.
Example Question #1 : How To Find An Angle In A Hexagon
There is a regular hexagon with a side length of 
cannot be determined
Given that the hexagon is a regular hexagon, this means that all the side length are congruent and all internal angles are congruent. The question requires us to solve for the measure of an internal angle. Given the aforementioned definition of a regular polygon, this means that there must only be one correct answer.
In order to solve for the answer, the question provides additional information that isn't necessarily required. The measure of an internal angle can be solved for using the equation:


In this case, 
For this problem, the information about the side length may be negated.
Certified Tutor
All Intermediate Geometry Resources