We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #7 : How To Find The Area Of A Pentagon

A regular pentagon has a side length of and an apothem length of 4.8 . Find the area of the pentagon.

Possible Answers:

sq. units

16.8 sq. units

sq. units

133.6 sq. units

33.6 sq. units

Correct answer:

sq. units

Explanation:

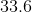
By definition a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 4.8 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{7\times 4.8}{2}=\frac{33.6}{2}=16.8$

Note: 16.8 is only the measurement for one of the five interior triangles. Thus, the solution is:

$16.8\times5=84$

Report an Error

Example Question #2 : How To Find The Area Of A Pentagon

A regular pentagon has a perimeter of and an apothem length of 8.9 . Find the area of the pentagon.

Possible Answers:

289.25

275.85

57.85

280.50

Correct answer:

289.25

Explanation:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:

p=5(s)

65=5(s)

$s=\frac{65}{5}=13$

Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of 8.9 .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{8.9\times 13}{2}=\frac{115.7}{2}=57.85$

Thus, the area of the entire pentagon is:

$A=57.85\times 5=289.25$

Report an Error

Example Question #791 : Plane Geometry

Pentagon_series_vt_custom_

Find the area of the pentagon shown above.

Possible Answers:

180 sq. units

184 sq. units

sq. units

198 sq. units

189 sq. units

Correct answer:

198 sq. units

Explanation:

To find the area of this pentagon, divide the interior of the pentagon into a four-sided rectangle and two right triangles. The area of the bottom rectangle can be found using the formula:

$A=width\times length$

$A=18\times8=144$

The area of the two right triangles can be found using the formula:

$A=\frac{base\times height}{2}$

$A=\frac{9\times 6}{2}=\frac{54}{2}=27$

Since there are two right triangles, the sum of both will equal the area of the entire triangular top portion of the pentagon.

Thus, the solution is:

A=144+27+27=198

Report an Error

Example Question #792 : Plane Geometry

A regular pentagon has a perimeter of 145 and an apothem length of . Find the area of the pentagon.

Possible Answers:

1,450 sq. units

1,500 sq. units

1,580 sq. units

580 sq. units

450 sq. units

Correct answer:

1,450 sq. units

Explanation:

To solve this problem, first work backwards using the perimeter formula for a regular pentagon:

p=5(s)

145=5(s)

$s=\frac{145}{5}=29$

Now you have enough information to find the area of this regular triangle.
Note: a regular pentagon must have equal sides and equivalent interior angles.

This question provides the length of the apothem of the pentagon—which is the length from the center of the pentagon to the center of a side. This information will allow us to divide the pentagon into equivalent interior triangles. Each triangle will have a base of and a height of .

The area of this pentagon can be found by applying the area of a triangle formula:

$A=\frac{base\times height}{2}$

$A=\frac{29\times 20}{2}=\frac{580}{2}=290$

Thus, the area of the entire pentagon is:

$A=290\times 5=1,450$

Report an Error

Example Question #11 : How To Find The Area Of A Pentagon

Find the area of the regular pentagon.

Possible Answers:

None of these

Correct answer:

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(3)$

$\text{Perimeter}=15$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(2)(15)$

$\text{Area of Pentagon}=15$

Report an Error

Example Question #792 : Intermediate Geometry

Find the area of the regular pentagon.

Possible Answers:

400

390

420

380

Correct answer:

420

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(14)$

$\text{Perimeter}=70$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(12)(70)$

$\text{Area of Pentagon}=420$

Report an Error

Example Question #15 : How To Find The Area Of A Pentagon

Find the area of the regular pentagon.

Possible Answers:

Correct answer:

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(8)$

$\text{Perimeter}=40$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(5)(40)$

$\text{Area of Pentagon}=60$

Report an Error

Example Question #16 : How To Find The Area Of A Pentagon

Find the area of the regular pentagon.

Possible Answers:

Correct answer:

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(7)$

$\text{Perimeter}=35$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(4)(35)$

$\text{Area of Pentagon}=70$

Report an Error

Example Question #17 : How To Find The Area Of A Pentagon

Find the area of the regular pentagon.

Possible Answers:

630

560

700

420

Correct answer:

560

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(16)$

$\text{Perimeter}=80$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(14)(80)$

$\text{Area of Pentagon}=560$

Report an Error

Example Question #793 : Intermediate Geometry

Find the area of the regular pentagon.

Possible Answers:

370

340

355

325

Correct answer:

325

Explanation:

Recall that the area of regular polygons can be found using the following formula:

$\text{Area of Regular Polygon}=\frac{1}{2}(\text{apothem})(\text{perimeter})$

First, find the perimeter of the pentagon. Since it is a regular pentagon, we can use the following formula to find its perimeter:

$\text{Perimeter}=5(\text{side length})$

Substitute in the length of the given side of the pentagon in order to find the perimeter.

$\text{Perimeter}=5(13)$

$\text{Perimeter}=65$

Next, substitute in the given and calculated information to find the area of the pentagon.

$\text{Area of Pentagon}=\frac{1}{2}(10)(65)$

$\text{Area of Pentagon}=325$

Report an Error

View Tutors

Michele
Certified Tutor

Georgian Court University, Bachelor in Arts, English. Georgian Court University, Master of Arts, Elementary and Middle School...

View Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View Tutors

Sahibzada
Certified Tutor

Northwestern University, Bachelor of Science, Materials Engineering.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Boston, English Tutors in Atlanta, Biology Tutors in San Francisco-Bay Area, Chemistry Tutors in Phoenix, Biology Tutors in Washington DC, Algebra Tutors in Atlanta, SSAT Tutors in Washington DC, Calculus Tutors in Phoenix, English Tutors in Los Angeles, Spanish Tutors in New York City

Popular Courses & Classes

Spanish Courses & Classes in Chicago, LSAT Courses & Classes in Denver, ACT Courses & Classes in Houston, ACT Courses & Classes in Washington DC, GMAT Courses & Classes in Houston, ISEE Courses & Classes in San Diego, SAT Courses & Classes in Houston, ACT Courses & Classes in Phoenix, ISEE Courses & Classes in Phoenix, LSAT Courses & Classes in Chicago

Popular Test Prep

MCAT Test Prep in Miami, SSAT Test Prep in Seattle, ACT Test Prep in Phoenix, SAT Test Prep in Atlanta, ACT Test Prep in Houston, SAT Test Prep in San Francisco-Bay Area, GRE Test Prep in Chicago, ACT Test Prep in Denver, GRE Test Prep in San Francisco-Bay Area, ACT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #7 : How To Find The Area Of A Pentagon

Example Question #2 : How To Find The Area Of A Pentagon

Example Question #791 : Plane Geometry

Example Question #792 : Plane Geometry

Example Question #11 : How To Find The Area Of A Pentagon

Example Question #792 : Intermediate Geometry

Example Question #15 : How To Find The Area Of A Pentagon

Example Question #16 : How To Find The Area Of A Pentagon

Example Question #17 : How To Find The Area Of A Pentagon

Example Question #793 : Intermediate Geometry

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: