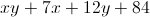Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #32 : Parallelograms

Given: Regular Pentagon PENTA with center . Construct segments $\overline{CP}$ and $\overline{CN}$ to form Quadrilateral CPEN .

True or false: Quadrilateral CPEN is a parallelogram.

Possible Answers:

True

False

Correct answer:

False

Explanation:

Below is regular Pentagon PENTA with center , a segment drawn from to each vertex - that is, each of its radii drawn.

Pentagon a

The measure of each angle of a regular pentagon can be calculated by setting equal to 5 in the formula

$\frac{(N-2)180^{\circ }}{N}$

and evaluating:

$\frac{(5-2)180^{\circ }}{5} = \frac{3 \cdot 180^{\circ }}{5} = \frac{540^{\circ }}{5} = 108^{\circ }$

Specifically,

$m \angle PEN = 108 ^{\circ }$

By symmetry, each radius bisects one of these angles. Specifically,

$m \angle CPE = \frac{1}{2} m \angle APE = \frac{1}{2} \cdot 108^{\circ } = 54 ^{\circ }$

By the Same-Side Interior Angles Theorem, consecutive angles of a parallelogram are supplementary - that is, their measures total $180^{\circ }$ . However,

$m \angle PEN + m \angle CPE = 108 ^{\circ } + 54 ^{\circ } = 162^{\circ }$ ,

violating these conditions. Therefore, Quadrilateral CPEN is not a parallelogram.

Report an Error

Example Question #371 : Plane Geometry

Given: Quadrilateral ABCD such that $m \angle A = 80 ^{\circ }$ and $m \angle B = 100^{\circ }$ .

True or false: It follows that Quadrilateral ABCD is a parallelogram.

Possible Answers:

False

True

Correct answer:

False

Explanation:

$m \angle A + m \angle B = 80^{\circ } +100 ^{\circ } = 180^{\circ }$ , making $\angle A$ and $\angle B$ supplementary. By the Converse of the Same Side Interior Angles Theorem, , it does follow that $\overline{AD} || \overline{BC}$ . However, without knowing the measures of the other two angles, nothing further can be concluded about Quadrilateral ABCD . Below are a parallelogram and a trapezoid, both of which have these two angles of these measures.

Parallelograms

Report an Error

Example Question #12 : How To Find An Angle In A Parallelogram

Given: Parallelogram ABCD such that $\angle A \cong \angle B$ and $\angle C \cong \angle D$ .

True or false: It follows that Parallelogram ABCD is a rectangle.

Possible Answers:

False

True

Correct answer:

True

Explanation:

By the Same-Side Interior Angles Theorem, consecutive angles of a parallelogram can be proved to be supplementary - that is, their angle measures total $180^{\circ }$ . Specifically, $\angle A$ and $\angle B$ are a pair of supplementary angles. Since they are also congruent, it follows that both are right angles. For the same reason, $\angle C$ and $\angle D$ are also right angles. The parallelogram, having four right angles, is a rectangle by definition.

Report an Error

Example Question #371 : Plane Geometry

Given: Rectangle ABCD with diagonals $\overline{AC}$ and $\overline{BD}$ intersecting at point .

True or false: $\angle AXB$ must be a right angle.

Possible Answers:

True

False

Correct answer:

False

Explanation:

The diagonals of a parallelogram are perpendicular - and, consequently, $\angle AXB$ is a right angle. - if and only if the parallelogram is a rhombus, a figure with four sides of equal length. Not all rectangles have four congruent sides. Therefore, $\angle AXB$ need not be a right angle.

Report an Error

Example Question #202 : Quadrilaterals

Given: Parallelogram ABCD such that $m \angle A = 90^{\circ }$ .

True or false: Parallelogram ABCD must be a rectangle.

Possible Answers:

False

True

Correct answer:

True

Explanation:

A rectangle is a parallelogram with four right angles.

Consecutive angles of a parallelogram are supplementary. If one angle of a parallelogram is given to be right, then its neighboring angles, being supplementary to a right angle, are right as well; also, opposite angles of a parallelogram are congruent, so the opposite angle is also right. All four angles must be right, making the parallelogram a rectangle by definition.

Report an Error

Example Question #371 : Intermediate Geometry

Find the perimeter of the following box in inches:

Geo_box

Possible Answers:

12x +7y

x + y + 19

2x + 2y + 38

xy + 7x + 12y +84

84xy

Correct answer:

2x + 2y + 38

Explanation:

The answer is 2x + 2y + 38 .

You can find the perimeter by adding all of its respective sides as such:

(12 + x) + (12 + x) + (7 + y) + (7 + y) .

Adding like terms will result in

2x + 2y + 38

If you chose xy + 7x + 12y +84 , you multiplied the two sides to find the area.

If you chose x + y + 19 , you only added two sides. Perimeter involves all 4 sides; so double the width and length.

Just remember, the width is 12 added to . Not 12 times the side of .

Report an Error

Example Question #31 : Parallelograms

A parallelogram has an area of $54\:cm^2$ . If the height is $6\:cm$ , what is the length of the base?

Possible Answers:

$4.5\:cm$

Cannot be determined

$12\:cm$

$18\:cm$

$9\:cm$

Correct answer:

$9\:cm$

Explanation:

If the area of a parallelogram is given as $54\:cm^2$ with a height of $6\:cm$ , we can refer back to the equation for the area of a parallelogram:

$A= b \cdot h$ , where is height and is the length of the base.

This very quickly becomes a problem of substituting in values and finding the value of an unknown variable, in this case, :

$54\:cm^2=6\:cm \cdot b$

$\frac{54\:cm^2}{6\:cm}=b$

$b=9\:cm$

Report an Error

Example Question #371 : Intermediate Geometry

A parallelogram has a base of 10in and an area of 35in^2 . What is the height of the parallelogram?

Possible Answers:

3.5in

3in

3.25in

1.25in

Correct answer:

3.5in

Explanation:

In order to find the height of this parallelogram apply the formula: $A=base\times height$

$35=10\times height$

$height= \frac{35}{10}=3.5$

Report an Error

Example Question #4 : How To Find The Length Of The Side Of A Parallelogram

A parallelogram has a height of 12ft and an area of 168ft^2 . What is the length of the base of the parallelogram?

Possible Answers:

15ft

14ft

12ft

10ft

Correct answer:

14ft

Explanation:

To find the missing side of this parallelgram apply the formula: $A=base\times height$

Thus, the solution is:

$168=12\times base$

$base=\frac{168}{12}=14$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

Given that a parallelogram has a height of 2.5ft and an area of 20ft^2 . Find the base of the parallelogram.

Possible Answers:

12ft

7.5ft

6.5ft

8ft

Correct answer:

8ft

Explanation:

In order to find the base of this parallelogram apply the formula: $Area=base\times height$

Thus, the solution is:

$20=base\times2.5$

$base=\frac{20}{2.5}$

base=8

Report an Error

View Tutors

Yaakoub
Certified Tutor

CUNY Queens College, Bachelor of Science, Finance. Vaughn College of Aeronautics and Technology, Bachelor of Science, Electri...

View Tutors

Jasmine
Certified Tutor

Mercer University, Bachelor of Science, Biochemistry. Mercer University, Master of Science, Biomedical Sciences.

View Tutors

Kelsey
Certified Tutor

Gonzaga University, Bachelor in Arts, English. Western Governors University, Master of Arts Teaching, High School Teaching.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Atlanta, ISEE Tutors in Los Angeles, Spanish Tutors in San Diego, Calculus Tutors in Houston, LSAT Tutors in Phoenix, Chemistry Tutors in Houston, GMAT Tutors in Phoenix, LSAT Tutors in Chicago, LSAT Tutors in Miami, Math Tutors in Dallas Fort Worth

Popular Courses & Classes

GMAT Courses & Classes in Denver, Spanish Courses & Classes in Denver, Spanish Courses & Classes in Washington DC, Spanish Courses & Classes in Miami, GMAT Courses & Classes in Washington DC, LSAT Courses & Classes in Boston, Spanish Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Houston, LSAT Courses & Classes in Seattle, GMAT Courses & Classes in Phoenix

Popular Test Prep

ISEE Test Prep in New York City, ISEE Test Prep in Philadelphia, SSAT Test Prep in Phoenix, SAT Test Prep in Philadelphia, LSAT Test Prep in Chicago, SSAT Test Prep in San Diego, ACT Test Prep in Denver, GMAT Test Prep in Miami, GMAT Test Prep in Phoenix, SAT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #32 : Parallelograms

Example Question #371 : Plane Geometry

Example Question #12 : How To Find An Angle In A Parallelogram

Example Question #371 : Plane Geometry

Example Question #202 : Quadrilaterals

Example Question #371 : Intermediate Geometry

Example Question #31 : Parallelograms

Example Question #371 : Intermediate Geometry

Example Question #4 : How To Find The Length Of The Side Of A Parallelogram

Example Question #2 : How To Find The Length Of The Side Of A Parallelogram

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: