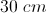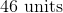Intermediate Geometry : Intermediate Geometry
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : How To Find The Perimeter Of A Rhombus
Given a rhombus with diagonal lengths of 12cm and 16cm, find the perimeter.
A rhombus is a parallelogram with all of its sides being equal. A square is a rhombus with all of the angles being equal as well as all of the sides. Both squares and rhombuses have perpendicular diagonal bisectors that split each diagonal into 2 equal pieces, and also splitting the quadrilateral into 4 equal right triangles.
With this being said, we know the Pythagorean Theorem would work great in this situation, using half of each diagonal as the two legs of the right triangle.
We find the hypotenuse to be 10cm. Since the hypotenuse of each triangle is a side of the rhombus, we have found what we need to find the perimeter.
Each side is the same, so we add all 4 sides to find the perimeter.
Example Question #1 : How To Find The Perimeter Of A Rhombus
The diagonals of a rhombus have lengths 
We should begin with a picture.
We should recall several things. First, all four sides of a rhombus are congruent, meaning that if we find one side, we can simply multiply by four to find the perimeter. Second, the diagonals of a rhombus are perpendicular bisectors of each other, thus giving us four right triangles and splitting each diagonal in half. We therefore have four congruent right triangles. Using Pythagorean Theorem on any one of them will give us the length of our sides.
With a side length of 17, our perimeter is easy to obtain.
Our perimeter is 68 units.
Example Question #11 : Rhombuses
A rhombus has an area of 
In order to solve this problem, use the given information to work backwards to find a side length of the rhombus:
Then apply the perimeter formula:
Example Question #2 : How To Find The Perimeter Of A Rhombus
A rhombus has an area of 
In order to solve this problem, use the given information to work backwards to find a side length of the rhombus:
Since, perimeter 
Perimeter=
Example Question #1 : How To Find The Perimeter Of A Rhombus
A rhombus has a side length of 
To find the perimeter, apply the formula: 
Example Question #1 : How To Find The Perimeter Of A Rhombus
A rhombus has an area of 
In order to solve this problem, use the given information to work backwards to find a side length of the rhombus: 
Example Question #7 : How To Find The Perimeter Of A Rhombus
Given that a rhombus has a side length of 
To find the perimeter of this rhombus, apply the formula: 
Example Question #2 : How To Find The Perimeter Of A Rhombus
A rhombus has an area of 
In order to solve this problem, use the given information to work backwards to find a side length of the rhombus: 
Example Question #9 : How To Find The Perimeter Of A Rhombus
A rhombus has a side length of 
To find the perimeter, first convert 
Then apply the formula 
Since,
The solution is:
Example Question #3 : How To Find The Perimeter Of A Rhombus
Find the perimeter of a rhombus that has a side length of 
In order to find the perimeter of this rhombus, first convert 
Then apply the formula: 
Since, 
All Intermediate Geometry Resources
