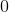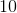Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #2 : How To Find The Equation Of A Tangent Line

Find the equation for the tangent line at (-3,8) for the circle (x+4)^2 + (y - 2 )^2 = 37 .

Possible Answers:

$y = \frac{7}{6} x + 11 \frac{1}{2}$

$y = -\frac{1}{6} x + 7\frac{1}{2 }$

$y = -\frac{1}{6} x + 2\frac{2}{3}$

y = 6x + 10

$y = -\frac{7}{6}x + 4 \frac{1}{2}$

Correct answer:

$y = -\frac{1}{6} x + 2\frac{2}{3}$

Explanation:

The circle's center is (-4, 2) . The tangent line will be perpendicular to the line going through the points (-4,2) and (-3, 8) , so it will be helpful to know the slope of this line:

$\frac{ \Delta y }{ \Delta x } = \frac{ 8-2 }{ -3+4 } = \frac{ 6 }{ 1 }$

Since the tangent line is perpendicular, its slope is $-\frac{1}{6 }$

To write the equation in the form y = mx + b , we need to solve for "b," the y-intercept. We can plug in the slope for "m" and the coordinates of the point (-3, 8 ) for x and y:

$8= -\frac{1}{6}(-3) + b$

$8 = \frac{1} { 2 } + b$

$7 \frac{1}{2} = b$

The equation is $y = -\frac{1}{6} x+7 \frac{1}{2}$

Report an Error

Example Question #2 : How To Find The Equation Of A Tangent Line

Find the equation for the tangent line of the circle (y+1)^2 + (x- 4 ) ^ 2 = 8 at the point (-2, 3 ) .

Possible Answers:

$y = -\frac{2}{3} x + \frac{13}{3 }$

$y = -\frac{3}{2}x$

$y = \frac{3}{2} x + 6$

$y = -\frac{2}{3} x - \frac{5}{3}$

$y = \frac{3}{2 } x - 2\frac{1}{2}$

Correct answer:

$y = \frac{3}{2} x + 6$

Explanation:

The circle's center is (4, -1) . The tangent line will be perpendicular to the line going through the points (4, -1 ) and (-2,3) , so it will be helpful to know the slope of this line:

$\frac{ \Delta y }{ \Delta x } = \frac{-1 - 3 }{ 4 - - 2 } = \frac{-4}{6 } = -\frac{2}{3}$

Since the tangent line is perpendicular, its slope is $\frac{3}{2 }$ .

To write the equation in the form y = mx + b , we need to solve for "b," the y-intercept. We can plug in the slope for "m" and the coordinates of the point (-2,3) for x and y:

$3= \frac{3}{2}(-2) + b$

3=-3 + b

6= b

The equation is $y = \frac{3}{2} x +6$

Report an Error

Example Question #3 : How To Find The Equation Of A Tangent Line

Find the equation for the tangent line to the circle (y+ 2 )^2 + (x -3)^2 = 169 at the point (15, 3 ) .

Possible Answers:

$y = -\frac{12}{5} x + 39$

y = -12x + 183

y = -18x + 69

$y = -\frac{12} {5 } x + \frac{26}{5 }$

y = -18x + 273

Correct answer:

$y = -\frac{12}{5} x + 39$

Explanation:

The circle's center is (3, -2) . The tangent line will be perpendicular to the line going through the points (3, -2) and (15,3) , so it will be helpful to know the slope of this line:

$\frac{ \Delta y }{ \Delta x } = \frac{ 3 --2 }{ 15 -3 } = \frac{ 5 }{ 12 }$

Since the tangent line is perpendicular, its slope is $-\frac{12}{5 }$

To write the equation in the form y = mx + b , we need to solve for "b," the y-intercept. We can plug in the slope for "m" and the coordinates of the point (15,3 ) for x and y:

$3 = -\frac{12}{5}(15) + b$

3 = -36+ b

39 = b

The equation is $y = - \frac{12}{5} x+39$

Report an Error

Example Question #8 : How To Find The Equation Of A Tangent Line

Circle

Refer to the above diagram,

Give the equation of the line tangent to the circle at the point shown.

Possible Answers:

$y = -\frac{9}{4}x+ 13$

$y = \frac{4}{9} x+ \frac{65}{9}$

None of the other choices gives the correct response.

$y = -\frac{4}{9} x+ \frac{97}{9}$

$y = \frac{9}{4}x$

Correct answer:

$y = -\frac{4}{9} x+ \frac{97}{9}$

Explanation:

The tangent to a circle at a given point is perpendicular to the radius that has the center and the given point as its endpoints.

The circle has its center at origin (0,0) ; since this and (4,9) are the endpoints of the radius - and the line that includes this radius includes both points - its slope can be found by setting $x_{1} = y_{1} = 0 , x_{2}= 4, y_{2} = 9$ in the following slope formula:

$m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}$

$m = \frac{9-0}{4-0} = \frac{9 }{4 }$

The tangent line, being perpendicular to this radius, has as its slope the opposite of the reciprocal of this, which is $m = -\frac{4}{9}$ . Since the tangent line includes point (4, 9) , set $m = -\frac{4}{9}, x_{1} = 4, y_{1} = 9$ in the point-slope formula and simplify:

$y - y_{1} = m (x-x_{1})$

$y - 9= -\frac{4}{9} (x-4)$

$y - 9= -\frac{4}{9} \cdot x- \left (-\frac{4}{9} \right ) \cdot 4$

$y - 9= -\frac{4}{9} x+ \frac{16}{9}$

$y - 9+ 9 = -\frac{4}{9} x+ \frac{16}{9} + 9$

$y = -\frac{4}{9} x+ \frac{16}{9} + \frac{81}{9}$

$y = -\frac{4}{9} x+ \frac{97}{9}$

Report an Error

Example Question #1 : How To Find The Equation Of A Tangent Line

A line is tangent to the circle $(x-4)^{2} + (y-2)^{2} = 100$ at the point (10,-6)

What is the equation of this line?

Possible Answers:

$y= \frac{4}{3}x-\frac{58}{3}$

$y= -\frac{4}{3}x+\frac{22}{3}$

None of the other answers are correct.

$y= \frac{3}{4}x-\frac{27}{2}$

$y=- \frac{3}{4}x+\frac{3}{2}$

Correct answer:

$y= \frac{3}{4}x-\frac{27}{2}$

Explanation:

The center of this circle is (4,2)

Therefore, the radius with endpoint (10,-6) has slope

$\frac{2-(-6)}{4-10}= \frac{8}{-6}= -\frac{4}{3}$

The tangent line at (10,-6) is perpendicular to this radius; therefore, its slope is the opposite of the reciprocal of $-\frac{4}{3}$ , or $\frac{3}{4}$ .

Now use the point-slope formula with this slope and the point of tangency:

$y-(-6)= \frac{3}{4} \left ( x-10\right )$

$y+6= \frac{3}{4}x-\frac{15}{2}$

$y= \frac{3}{4}x-\frac{27}{2}$

Report an Error

Example Question #1 : How To Find The Slope Of A Tangent Line

What is the slope of the tangent line to the graph of y=x^2-6 when x=3 ?

Possible Answers:

Correct answer:

Explanation:

To find the slope of the tangent line, first we must take the derivative of x^2-6 , giving us . Next we simply plug in our given x-value, which in this case is x=3 . This leaves us with a slope of .

Report an Error

Example Question #1501 : Intermediate Geometry

Suppose the equation of a line is -3x+5y=-3 . What is the slope of the tangent line at x=3 ?

Possible Answers:

$\frac{3}{5}$

$\frac{5}{3}$

$\frac{9}{5}$

$-\frac{9}{5}$

Correct answer:

$\frac{3}{5}$

Explanation:

Rewrite -3x+5y=-3 in slope-intercept form, y=mx+b .

5y=3x-3

$y=\frac{3}{5}x-\frac{3}{5}$

The slope of the tangent line is $\frac{3}{5}$ .

Report an Error

Example Question #1502 : Intermediate Geometry

Suppose a function y=1 . What is the slope of the tangent line at x=10 ?

Possible Answers:

$\textup{There is no slope.}$

Correct answer:

Explanation:

Write the formula for slope-intercept form.

y=mx+b

m=0

The slope of y=1 is always zero at every point on the domain. Therefore, the slope at x=10 must also be zero.

Report an Error

Example Question #1 : How To Find X Or Y Intercept

Given the line 3x+4y=24 what is the sum of the and intercepts?

Possible Answers:

Correct answer:

Explanation:

The intercepts cross an axis.

For the intercept, set x=0 to get y=6

For the intercept, set y=0 to get x=8

So the sum of the intercepts is .

Report an Error

Example Question #3 : X And Y Intercept

What are the and -intercepts of the line defined by the equation:

y = 3x + 6

Possible Answers:

(-2,0) (0,6)

(0,-6) (0,0)

(0,0) (0,0)

(0,6) (2,0)

(2,0) (2,-6)

Correct answer:

(-2,0) (0,6)

Explanation:

To find the intercepts of a line, we must set the and values equal to zero and then solve.

0 = 3x +6

-6 = 3x

x = -2

(-2, 0)

y = 3 (0) + 6

y = 6

(0, 6)

Report an Error

View Tutors

Kisa
Certified Tutor

University of Toronto, Scarborough, Bachelor, Public Policy.

View Tutors

Rasha
Certified Tutor

George Washington University, Bachelor of Science, Health Sciences, General. Shenandoah University, Pharmaceutical Chemist, P...

View Tutors

Jacob
Certified Tutor

College of Saint Benedict and Saint John's University, Bachelor of Science, Physics.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in Washington DC, SAT Tutors in San Diego, Biology Tutors in New York City, LSAT Tutors in San Diego, Computer Science Tutors in Dallas Fort Worth, Computer Science Tutors in Houston, ISEE Tutors in Houston, Biology Tutors in Denver, Computer Science Tutors in Philadelphia, LSAT Tutors in Miami

Popular Courses & Classes

MCAT Courses & Classes in New York City, ACT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Houston, SSAT Courses & Classes in Miami, Spanish Courses & Classes in Denver, GMAT Courses & Classes in Chicago, GRE Courses & Classes in Denver, SAT Courses & Classes in Denver, GRE Courses & Classes in Phoenix

Popular Test Prep

GMAT Test Prep in Chicago, MCAT Test Prep in Chicago, GMAT Test Prep in Miami, ACT Test Prep in Philadelphia, ACT Test Prep in San Francisco-Bay Area, SAT Test Prep in Atlanta, ACT Test Prep in San Diego, MCAT Test Prep in Denver, GRE Test Prep in New York City, MCAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Intermediate Geometry

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #2 : How To Find The Equation Of A Tangent Line

Example Question #2 : How To Find The Equation Of A Tangent Line

Example Question #3 : How To Find The Equation Of A Tangent Line

Example Question #8 : How To Find The Equation Of A Tangent Line

Example Question #1 : How To Find The Equation Of A Tangent Line

Example Question #1 : How To Find The Slope Of A Tangent Line

Example Question #1501 : Intermediate Geometry

Example Question #1502 : Intermediate Geometry

Example Question #1 : How To Find X Or Y Intercept

Example Question #3 : X And Y Intercept

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: