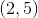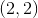Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Lines

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 … 22 23 Next →

Example Question #21 : Coordinate Geometry

Find the midpoint of a line segment that has endpoints at $\left(\frac{1}{2}, 5\right)$ and $\left(-\frac{3}{2}, 1\right)$ .

Possible Answers:

$(-\frac{1}{2}, -\frac{1}{2})$

$(-\frac{3}{4}, 6)$

$(-\frac{1}{2}, 3)$

$(-\frac{1}{2}, 2)$

Correct answer:

$(-\frac{1}{2}, 3)$

Explanation:

Recall the formula for finding a midpoint of a line segment:

$\text{Midpoint}=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$

The coordinates of the midpoint is just the average of the x-coordinates and the average of the y-coordinates.

Plug in the given points to find the midpoint of the line segment.

$\text{Midpoint}=(\frac{\frac{1}{2}-\frac{3}{2}}{2}, \frac{5+1}{2})=(-\frac{1}{2}, 3)$

Report an Error

Example Question #22 : Coordinate Geometry

Find the midpoint of a line segment that has endpoints at (9, 120) and (-24, 2) .

Possible Answers:

$(-\frac{15}{2}, 61)$

$(\frac{15}{2}, 61)$

$(-\frac{15}{2}, 59)$

$(-\frac{33}{2}, 60)$

Correct answer:

$(-\frac{15}{2}, 61)$

Explanation:

Recall how to find the midpoint of a line segment with endpoints at (x_1, y_1) and (x_2, y_2) :

$\text{Midpoint}=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$

$\text{Midpoint}=(\frac{9+(-24)}{2}, \frac{120+2}{2})=(-\frac{15}{2}, 61)$

Report an Error

Example Question #23 : Coordinate Geometry

Find the midpoint of a line segment that has endpoints at (16, 7) and (8, 9) .

Possible Answers:

(12, 8)

(4, -1)

(1, 8)

$(\frac{25}{2}, \frac{15}{2})$

Correct answer:

(12, 8)

Explanation:

Recall how to find the midpoint of a line segment with endpoints at (x_1, y_1) and (x_2, y_2) :

$\text{Midpoint}=(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2})$

$\text{Midpoint}=(\frac{16+8}{2}, \frac{7+9}{2})=(12, 8)$

Report an Error

Example Question #24 : Coordinate Geometry

A line segment on the coordinate plane has its endpoints at (3.8, -1.7) and (9.2, 5.5) .

True or false: Its midpoint is located at (6.5, 3.6) .

Possible Answers:

False

True

Correct answer:

False

Explanation:

The midpoint of a line segment with endpoints $(x_{1}, y_{1})$ and $(x_{2}, y_{2})$ is located at $\left ( \frac{x_{1}+x_{2}}{2} , \frac{y_{1}+ y_{2}}{2} \right )$ .

Set $x_{1}= 3.8, y_{1} =-1.7,x_{2} =9.2, y_{2}= 5.5$ , and evaluate both expressions:

$\frac{x_{1}+x_{2}}{2}= \frac{3.8+9.2}{2} = \frac{13}{2} = 6.5$

$\frac{-1.7+5.5}{2} =\frac{3.8}{2} = 1.9$

The midpoint is at (6.5, 1.9) , so the statement is false.

Report an Error

Example Question #1 : How To Find The Endpoints Of A Line Segment

Find the midpoint between the points:

(0,4) and (2,8)

Possible Answers:

(1,1)

(1,7)

(1,6)

(2,4)

(0,0)

Correct answer:

(1,6)

Explanation:

The midpoint formula is

$\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)$

So for our two points the equation is

$\left(\frac{0+2}{2},\frac{4+8}{2}\right)$

$\left(\frac{2}{2},\frac{12}{2}\right)$

(1,6)

Report an Error

Example Question #2 : How To Find The Endpoints Of A Line Segment

What is the midpoint between the two points:

(0,0) and (3,4)

Possible Answers:

(2,1.5)

(1.5,2)

(4,3)

(9,16)

(3,4)

Correct answer:

(1.5,2)

Explanation:

The midpoint formula is

$\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)$

If we plug in our points we get

$\left(\frac{0+3}{2},\frac{0+4}{2}\right)$

$\left(\frac{3}{2},\frac{4}{2}\right)$

(1.5,2)

Report an Error

Example Question #3 : How To Find The Endpoints Of A Line Segment

What is the midpoint between the two points:

(1,9) and (3, 5)

Possible Answers:

(7,2)

(2,7)

(3,4)

(2,5)

(1,9)

Correct answer:

(2,7)

Explanation:

The midpoint formula is

$\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)$

So lets plug in our two points, that gives us

$\left(\frac{1+3}{2},\frac{9+5}{2}\right)$

$\left(\frac{4}{2},\frac{14}{2}\right)$

(2,7)

Report an Error

Example Question #4 : How To Find The Endpoints Of A Line Segment

What is the midpoint between the two points:

(0,0) and (4,5)

Possible Answers:

(4,2.5)

(2,2)

(4,5)

(2,5)

(2,2.5)

Correct answer:

(2,2.5)

Explanation:

The equation to find the midpoint between two points is

$\left(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2}\right)$

If we plug in our values of the two points we get

$\left(\frac{0+4}{2},\frac{0+5}{2}\right)$

$\left(\frac{4}{2},\frac{5}{2}\right)$

(2,2.5)

Report an Error

Example Question #5 : How To Find The Endpoints Of A Line Segment

One of the endpoints of a line is $\small (8, -7)$ and the midpoint is $\small (1, -3)$ . What is the other endpoint?

Possible Answers:

$\small (15, 1 )$

$\small (-6, 1)$

$\small (-6, -11)$

$\small (15, -11)$

$\small (3, -1)$

Correct answer:

$\small (-6, 1)$

Explanation:

The midpoint's coordinates are the average of the endpoints'.

This means that the x-coordinates of the two endpoints have a mean of 1:

$\small \frac{8+x }{2} = 1$ multiply both sides by 2

$\small 8 + x = 2$ subtract 8

$\small x = -6$ this means the other endpoint's x-coordinate is -6

This also means that the y-coordinates of the two endpoints have a mean of -3:

$\small \frac{-7+y}{2} = -3$ multiply both sides by 2

$\small -7 + y = -6$ add 7 to both sides

$\small y = 1$

The coordinate pair that we're looking for is (-6, 1)

Report an Error

Example Question #6 : How To Find The Endpoints Of A Line Segment

The midpoint of a line is $\small (9, 9)$ and one of the endpoints is $\small (1, 17)$ . What is the other endpoint?

Possible Answers:

$\small (17, 25)$

$\small (17, 1)$

$\small (-7, 1 )$

$\small (8, -8)$

$\small (-7, 25)$

Correct answer:

$\small (17, 1)$

Explanation:

The midpoint's coordinates are just the mean of the endpoints'.

This means that the mean of the two x-coordinates is 9:

$\small \frac{x+ 1}{2} = 9$ multiply both sides by 2

$\small x + 1 = 18$ subtract 1

$\small x = 17$

This also means that the mean of the two y-coordinates is 9:

$\small \frac{y+17}{2} = 9$ multiply both sides by 2

$\small y + 17 = 18$ subtract 17

$\small y = 1$

So the other endpoint we were solving for is $\small (17, 1 )$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 … 22 23 Next →

View Tutors

Jirong
Certified Tutor

Nanjing University of Science and Technology, Bachelor of Science, Electrical Engineering. Cleveland State University, Master...

View Tutors

Daniel
Certified Tutor

Florida International University, Bachelor in Arts, English.

View Tutors

Harrison
Certified Tutor

Hamilton College, Bachelor in Arts, Mathematics. University of Connecticut, Master of Science, Applied Mathematics.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Los Angeles, LSAT Tutors in Phoenix, Physics Tutors in Seattle, English Tutors in Los Angeles, Chemistry Tutors in Dallas Fort Worth, English Tutors in New York City, SAT Tutors in Washington DC, Chemistry Tutors in Phoenix, Statistics Tutors in Seattle, French Tutors in Boston

Popular Courses & Classes

MCAT Courses & Classes in Miami, GRE Courses & Classes in San Diego, Spanish Courses & Classes in Miami, Spanish Courses & Classes in Washington DC, SSAT Courses & Classes in New York City, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Chicago, GMAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Miami, GRE Test Prep in Denver, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Denver, SAT Test Prep in Phoenix, SSAT Test Prep in Washington DC, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Denver, GMAT Test Prep in Boston, SSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Lines

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #21 : Coordinate Geometry

Example Question #22 : Coordinate Geometry

Example Question #23 : Coordinate Geometry

Example Question #24 : Coordinate Geometry

Example Question #1 : How To Find The Endpoints Of A Line Segment

Example Question #2 : How To Find The Endpoints Of A Line Segment

Example Question #3 : How To Find The Endpoints Of A Line Segment

Example Question #4 : How To Find The Endpoints Of A Line Segment

Example Question #5 : How To Find The Endpoints Of A Line Segment

Example Question #6 : How To Find The Endpoints Of A Line Segment

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: