Intermediate Geometry : Lines
Study concepts, example questions & explanations for Intermediate Geometry
All Intermediate Geometry Resources
Example Questions
Example Question #1 : Parallel Lines
If Angles 2 and 7 are congruent, line AB and CD are __________.
askance
perpendicular
parallel
skew
parallel
Lines AB and CD are parallel based on the Alternate Exterior Angle theorem.
Example Question #6 : Parallel Lines
If lines AB and CD are parallel, angles 5 and 1 are __________.
interior angles
exterior angles
corresponding angles
alternate exterior angles
alternate interior angles
corresponding angles
If the two lines are parallel, the transverse line makes it so that angles 2 and 7 are corresponding angles.
Example Question #181 : Lines
If lines AB and CD are parallel, the sum of Angle 6 plus Ange 4 equals __________.
15 deg
90 deg
45 deg
0 deg
180 deg
180 deg
If lines AB and CD are parallel, the sum of Angles 4 and 6 is 180 deg based on the Consecutive Interior Angle Theorem.
Example Question #182 : Lines
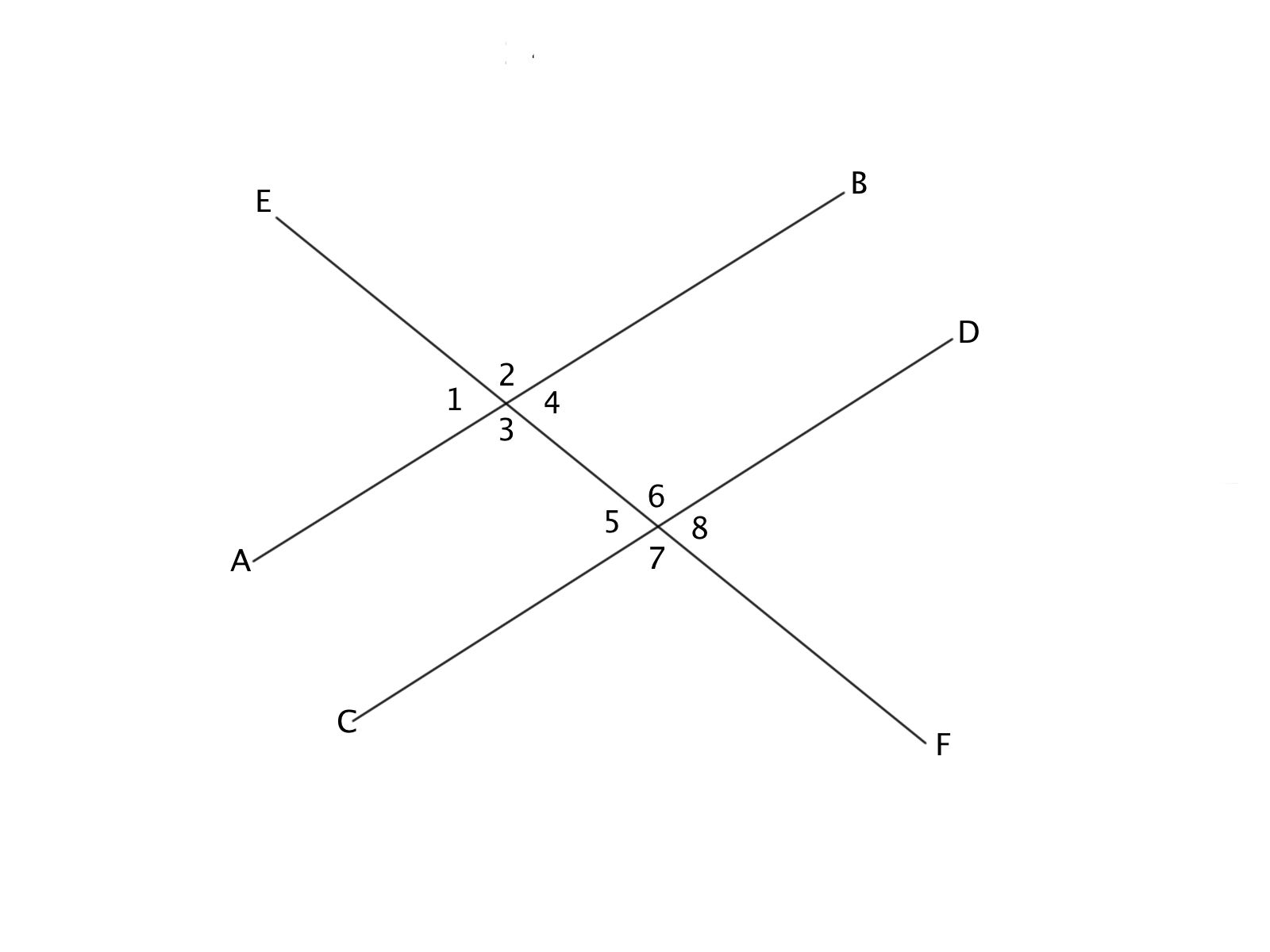
If lines AB and CD are parallel, angles 2 and 7 are congruent based on which theorem?
Consecutive Angles
Alternate Interior Angles
Corresponding Angles
There is not enough information to determine
Alternate Exterior Angles
Alternate Exterior Angles
Angles 2 and 7 are both on the exterior side of the transverse, this means they are Alternate Exterior Angles.
Example Question #183 : Lines
If lines AB and CD are parallel, which angles are congruent to Angle 3?
Angles 5, 8, and 1
Angles 1 and 5
Angles 2, 7, and 6
There is not enought information to determine
Angles 7 and 6
Angles 2, 7, and 6
Angle 2 is congruent based on the Vertical Angle Theorem. Angle 7 is congruent based on the Corresponding Angles Theorem. Angle 6 is congruent based on the Alternate Interior Angles theorem.
Example Question #182 : Lines
Where do the lines 
They never intersect.
They never intersect.
By solving both equations to standard form 
Example Question #11 : How To Find Out If Lines Are Parallel
A line passes through both the coordinates 
The line has a slope of 
Example Question #11 : How To Find Out If Lines Are Parallel
Choose the equation that represents a line that is parallel to 
Two lines are parallel if and only if they have the same slope. To find the slopes, we must put the equations into slope-intercept form, 
Example Question #184 : Coordinate Geometry
Which of the following lines are parallel?
None of these.
None of these.
None of these lines are parallel.
In order for lines to be parallel, the lines must NEVER cross. Lines with identical slopes never cross. An example of two parallel lines would be:
Note that only the slope determines if line are parallel.
Example Question #185 : Coordinate Geometry
Are the lines of the equations
and
parallel, perpendicular, or neither?
Parallel
Neither
Perpendicular
Parallel
Write each equation in the slope-intercept form 
The first equation,
is in the slope-intercept form 
The slope of the line of this equation is the 
The lines of both equations have the same slope, 
Certified Tutor
All Intermediate Geometry Resources
