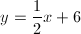Call Now to Set Up Tutoring:

(888) 888-0446

Intermediate Geometry : Lines

Study concepts, example questions & explanations for Intermediate Geometry

Create An Account

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #3 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

y=19x-14

Possible Answers:

y=-19x-2

$y=\frac{1}{19}x+14$

y=14x+19

y=19x+2

Correct answer:

y=19x+2

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, m=19 . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

y=19x+2

Report an Error

Example Question #4 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

y=129x-200

Possible Answers:

y=129x+41

$y=\frac{1}{129}x-2001$

y=-129x+200

y=200x-129

Correct answer:

y=129x+41

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, m=129 . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

y=129x+41

Report an Error

Example Question #9 : How To Find The Slope Of Parallel Lines

Find a line parallel to the line with the equation:

$y=\frac{1}{365}x-2$

Possible Answers:

y=365x-10

$y=\frac{x}{365}+4$

$y=-\frac{x}{365}+120$

y=-25x+124

Correct answer:

$y=\frac{x}{365}+4$

Explanation:

For two lines to be parallel, they must have the same slope. For a line in y=mx+b , or slope intercept form, corresponds to the slope of the line.

For the given line, $m=\frac{1}{365}$ . A line that is parallel must also then have the same slope.

Only the following line has the same slope:

$y=\frac{x}{365}+4$

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point (4, 2) ?

Possible Answers:

$\small y=\frac{1}{2}x+6$

$\small y=2x-6$

$\small y=\frac{1}{2}x$

$\small y=-2x+10$

Correct answer:

$\small y=\frac{1}{2}x$

Explanation:

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.

$\small 2=(\frac{1}{2})(4)+b$

$\small 2=2+b$

$\small b=0$

Therefore, the equation of the line is $\small y=\frac{1}{2}x$ .

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Suppose a line y=2x . What is the equation of a parallel line that intersects point (1,3) ?

Possible Answers:

y=2x+1

y=2x+4

y=2x+3

y=2x+5

y=2x+2

Correct answer:

y=2x+1

Explanation:

A line parallel to y=2x must have a slope of two. Given the point (1,3) and the slope, use the slope-intercept formula to determine the -intercept by plugging in the values of the point and solving for :

y=mx+b

3=(2)(1)+b

3=2+b

3-2=2+b-2

b=1

Plug the slope and the -intercept into the slope-intercept formula:

y=2x+1

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Find the equation of the line parallel to 3x+3y=1 that passes through the point (2,2) .

Possible Answers:

y=-x+4

y=x-2

y=3x+4

y=3x-4

y=-x-4

Correct answer:

y=-x+4

Explanation:

Write 3x+3y=1 in slope intercept form, y=mx+b , to determine the slope, :

3y=-3x+1

$y=-x+\frac{1}{3}$

The slope is:

m=-1

Given the slope, use the point (2,2) and the equation y=mx+b to solve for the value of the -intercept, . Substitute the known values.

2=(-1)(2)+b

b=4

With the known slope and the -intercept, plug both values back to the slope intercept formula. The answer is y=-x+4 .

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

Given y=3x+20 , find the equation of a line parallel.

Possible Answers:

$y=\frac{-1}{3}-20$

y=-3x-12

$y=\frac{1}{3}x-20$

y=3x-12

y=0.3x+20

Correct answer:

y=3x-12

Explanation:

The definition of a parallel line is that the lines have the same slopes, but different intercepts. The only answer with the same slope is y=3x-12 .

Report an Error

Example Question #1 : How To Find The Equation Of A Parallel Line

Which one of these equations is parallel to:

y=3x+4

Possible Answers:

y=-3x+7

$y=\frac{-1}{3}+4$

y=4

$y=\frac{1}{3}x$

y=3x+1

Correct answer:

y=3x+1

Explanation:

Equations that are parallel have the same slope.

For the equation:

y=3x+4

The slope is since that is how much changes with increment of .

The only other equation with a slope of is:

y=3x+1

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

What equation is parallel to:

y=x

Possible Answers:

y=x+42746

y=-x+1

y=2x

y=x^2+4

y=0

Correct answer:

y=x+42746

Explanation:

To find a parallel line to

y=x

we need to find another equation with the same slope of or .

The only equation that satisfies this is y=x+42746 .

Report an Error

Example Question #3 : How To Find The Equation Of A Parallel Line

What equation is parallel to:

y=5x+5

Possible Answers:

y=5x+10

$y=\frac{1}{5}x+4$

y=4x+3

y=x+5

$y=\frac{-1}{5}x+5$

Correct answer:

y=5x+10

Explanation:

To find an equation that is parallel to

y=5x+5

we need to find an equation with the same slope of .

Basically we are looking for another equation with .

The only other equation that satisfies this is

y=5x+10 .

Report an Error

View Tutors

Anatole
Certified Tutor

CUNY Hunter College, Bachelor in Arts, Multimedia.

View Tutors

Nicole
Certified Tutor

Western Governors University, Bachelor of Education, Special Education.

View Tutors

Nicole
Certified Tutor

Liberty University, Bachelor of Science, Psychology. Liberty University, Master of Arts, Mental Health Counseling.

All Intermediate Geometry Resources

8 Diagnostic Tests 250 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Reading Tutors in Philadelphia, GMAT Tutors in Washington DC, LSAT Tutors in Dallas Fort Worth, Statistics Tutors in Boston, Calculus Tutors in Philadelphia, Chemistry Tutors in San Francisco-Bay Area, ISEE Tutors in Miami, Algebra Tutors in Los Angeles, Statistics Tutors in Miami, Physics Tutors in Washington DC

Popular Courses & Classes

ISEE Courses & Classes in Philadelphia, SAT Courses & Classes in Boston, Spanish Courses & Classes in Miami, ISEE Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Boston, MCAT Courses & Classes in Phoenix, MCAT Courses & Classes in San Diego, SSAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Houston

Popular Test Prep

GRE Test Prep in Los Angeles, SAT Test Prep in Washington DC, SSAT Test Prep in Boston, ISEE Test Prep in Denver, LSAT Test Prep in Washington DC, ACT Test Prep in Denver, ACT Test Prep in Philadelphia, SAT Test Prep in Philadelphia, SAT Test Prep in Denver, LSAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Intermediate Geometry : Lines

Study concepts, example questions & explanations for Intermediate Geometry

All Intermediate Geometry Resources

Example Questions

Example Question #3 : How To Find The Slope Of Parallel Lines

Example Question #4 : How To Find The Slope Of Parallel Lines

Example Question #9 : How To Find The Slope Of Parallel Lines

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #3 : How To Find The Equation Of A Parallel Line

All Intermediate Geometry Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: