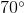Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Acute / Obtuse Triangles

In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?

Possible Answers:

$45^{\circ}$

$60^{\circ}$

$75^{\circ}$

$20^{\circ}$

$90^{\circ}$

Correct answer:

$60^{\circ}$

Explanation:

Since the sum of the angles of a triangle is $180^{\circ}$ , and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be , then the following expression could be written:

$x+3x+5x=180$

$9x=180$

$x=20$

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

Report an Error

Example Question #1 : Right Triangles

The measure of 3 angles in a triangle are in a 1:2:3 ratio. What is the measure of the middle angle?

Possible Answers:

Correct answer: 60

Explanation:

The angles in a triangle sum to 180 degrees. This makes the middle angle 60 degrees.

Report an Error

Example Question #3 : How To Find The Measure Of An Angle

Call the three angles of a triangle $\angle 1, \angle 2, \angle 3$ .

The measure of $\angle2$ is twenty degrees greater than that of $\angle 1$ ; the measure of $\angle 3$ is thirty degrees less than twice that of $\angle 1$ . If is the measure of $\angle 1$ , then which of the following equations would we need to solve in order to calculate the measures of the angles?

Possible Answers:

x + (x+20) = (2x+30)

x + (x-20) + 2(x-30) = 180

x + (x+20) + (2x-30) = 360

x + (x-20) + 2(x-30) = 360

x + (x+20) + (2x-30) = 180

Correct answer:

x + (x+20) + (2x-30) = 180

Explanation:

The measure of $\angle2$ is twenty degrees greater than the measure of $\angle 1$ , so its measure is 20 added to that of $\angle 1$ - that is, x + 2 0 .

The measure of $\angle 3$ is thirty degrees less than twice that of $\angle 1$ . Twice the measure of $\angle 1$ is , and thirty degrees less than this is 30 subtracted from - that is, 2x-30 .

The sum of the measures of the three angles of a triangle is 180, so, to solve for - thereby allowing us to calulate all three angle measures - we add these three expressions and set the sum equal to 180. This yields the equation:

x + (x+20) + (2x-30) = 180

Report an Error

Example Question #4 : How To Find The Measure Of An Angle

Call the three angles of a triangle $\angle 1, \angle 2, \angle 3$ .

The measure of $\angle2$ is forty degrees less than that of $\angle 1$ ; the measure of $\angle 3$ is ten degrees less than twice that of $\angle 1$ . If is the measure of $\angle 1$ , then which of the following equations would we need to solve in order to calculate the measures of the angles?

Possible Answers:

x + (x-40) + 2 (x - 10) = 180

x + (x-40) + (2x - 10) = 360

x + (x-40) = (2x - 10)

x + (x-40) + 2 (x - 10) = 360

x + (x-40) + (2x - 10) = 180

Correct answer:

x + (x-40) + (2x - 10) = 180

Explanation:

The measure of $\angle2$ is forty degrees less than the measure of $\angle 1$ , so its measure is 40 subtracted from that of $\angle 1$ - that is, x -40 .

The measure of $\angle 3$ is ten degrees less than twice that of $\angle 1$ . Twice the measure of $\angle 1$ is , and ten degrees less than this is 10 subtracted from - that is, 2x-10 .

x + (x-40) + (2x - 10) = 180

Report an Error

Example Question #4 : How To Find The Measure Of An Angle

Two interior angles of a triangle adds up to degrees. What is the measure of the other angle?

Possible Answers:

148

116

Correct answer:

116

Explanation:

The sum of the three angles of a triangle add up to 180 degrees. Subtract 64 degrees to determine the third angle.

180-64= 116

Report an Error

Example Question #1 : How To Find The Measure Of An Angle

What is $\frac{1}{5}$ of the measure of a right angle?

Possible Answers:

$18$^{\circ}$$

$45$^{\circ}$$

$450$^{\circ}$$

$85$^{\circ}$$

$22$^{\circ}$$

Correct answer:

$18$^{\circ}$$

Explanation:

A right angle has a measure of $90$^{\circ}$$ . One fifth of the angle is:

$\angle A=\frac{90}{5}= 18$^{\circ}$$

Report an Error

Example Question #6 : How To Find The Measure Of An Angle

What angle is complementary to $65$^{\circ}$$ ?

Possible Answers:

$130$^{\circ}$$

$25$^{\circ}$$

$115$^{\circ}$$

$65$^{\circ}$$

$35$^{\circ}$$

Correct answer:

$25$^{\circ}$$

Explanation:

To find the other angle, subtract the given angle from $90$^{\circ}$$ since complementary angles add up to $90$^{\circ}$$ .

The complementary is:

$\angle 90-\angle65 = \angle25$

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

What is the supplementary angle to $100$^{\circ}$$ ?

Possible Answers:

$170$^{\circ}$$

$10$^{\circ}$$

$280$^{\circ}$$

$70$^{\circ}$$

$80$^{\circ}$$

Correct answer:

$80$^{\circ}$$

Explanation:

Supplementary angles add up to $180$^{\circ}$$ . In order to find the correct angle, take the known angle and subtract that from $180$^{\circ}$$ .

$180$^{\circ}$ -100$^{\circ}$ = 80$^{\circ}$$

Report an Error

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

What angle is complement to $\frac{\pi}{6}$ ?

Possible Answers:

$\frac{\pi}{3}$

$\frac{\pi}{4}$

$\frac{2\pi}{3}$

$\frac{\pi}{6}$

$\frac{\pi}{9}$

Correct answer:

$\frac{\pi}{3}$

Explanation:

The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90. In this case, since we are given the angle in radians, we are subtracting from $\frac{\pi}{2}$ instead to find the complement. The conversion between radians and degrees is: $\pi \textup{ radians } = 180 \textup{ degrees}$

$\frac{\pi}{2}-\frac{\pi}{6}$

Reconvert the fractions to the least common denominator.

$\frac{\pi}{2}-\frac{\pi}{6} = \frac{3\pi}{6}-\frac{\pi}{6} = \frac{2\pi}{6}$

Reduce the fraction.

$\frac{2\pi}{6} = \frac{\pi}{3}$

Report an Error

Example Question #11 : How To Find The Measure Of An Angle

Spinner target 2

The above diagram shows a spinner. The radius of the smaller quarter-circles is half that of the larger quarter-circles.

A player spins the above spinner. What is the probability that the spinner will stop while pointing inside a red region?

Possible Answers:

$\frac{5}{13}$

$\frac{2}{7}$

$\frac{11}{24}$

$\frac{7}{24}$

Correct answer:

$\frac{7}{24}$

Explanation:

The size of the regions does not matter here. What matters is the angle measurement, or, equivalently, what part of a circle each sector is.

The two smaller red regions each comprise one fourth of one fourth of a circle, or

$\frac{1}{4} \times \frac{1}{4} = \frac{1}{16}$ circle.

The two larger red regions each comprise one third of one fourth of a circle, or

$\frac{1}{4} \times \frac{1}{3} = \frac{1}{12}$ circle.

Therefore, the total angle measure comprises

$\frac{1}{16} + \frac{1}{16} + \frac{1}{12} + \frac{1}{12}$

$=\frac{3}{48} + \frac{3}{48} + \frac{4}{48} + \frac{4}{48}$

$= \frac{14}{48} = \frac{7}{24}$

of a circle.

This makes $\frac{7}{24}$ the correct probability.

Report an Error

View Tutors

Jitendra
Certified Tutor

BHU, Bachelor, Mathematics.

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Kevin
Certified Tutor

St. Johns University, Bachelors, Math/Coaching.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Miami, SSAT Tutors in Houston, SSAT Tutors in San Diego, Physics Tutors in Dallas Fort Worth, Calculus Tutors in Los Angeles, Calculus Tutors in Houston, SSAT Tutors in Seattle, Statistics Tutors in Miami, Reading Tutors in Miami, LSAT Tutors in Philadelphia

Popular Courses & Classes

GRE Courses & Classes in Los Angeles, MCAT Courses & Classes in Seattle, SSAT Courses & Classes in Seattle, GRE Courses & Classes in Philadelphia, SAT Courses & Classes in Houston, Spanish Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in San Diego, GRE Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Los Angeles, SAT Courses & Classes in Miami

Popular Test Prep

ISEE Test Prep in Miami, MCAT Test Prep in Denver, ISEE Test Prep in Los Angeles, ISEE Test Prep in Boston, GMAT Test Prep in Los Angeles, ISEE Test Prep in Houston, ACT Test Prep in Washington DC, ACT Test Prep in Denver, GMAT Test Prep in Washington DC, MCAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Geometry

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #1 : Acute / Obtuse Triangles

Example Question #1 : Right Triangles

Example Question #3 : How To Find The Measure Of An Angle

Example Question #4 : How To Find The Measure Of An Angle

Example Question #4 : How To Find The Measure Of An Angle

Example Question #1 : How To Find The Measure Of An Angle

Example Question #6 : How To Find The Measure Of An Angle

Example Question #11 : How To Find The Measure Of An Angle

Example Question #1 : Solve Simple Equations For An Unknown Angle In A Figure: Ccss.Math.Content.7.G.B.5

Example Question #11 : How To Find The Measure Of An Angle

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: