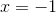All HSPT Math Resources
Example Questions
Example Question #411 : How To Find The Solution To An Equation
Solve for 
Example Question #922 : Concepts
Solve for 
Example Question #311 : Algebra
Multiply:
Multiply the whole numbers, and add an exponent to the variable totalling the amount of exponents in the equation:
Answer:
Example Question #312 : Algebra
Multiply:
Multiply the whole numbers, adding an exponent to the variable totalling the amount of variables in the equation:
Answer:
Example Question #311 : Algebra
Multiply:
Answer: 169
Example Question #921 : Concepts
Multiply the whole numbers and add an exponent to the variable totalling the amount of variables in the equation:
Answer:
Example Question #922 : Concepts
Multiply the whole numbers and add an exponent to the variable totaling the number of variables in the equation:
Answer:
Example Question #923 : Concepts
Multiply:
Multiply the whole numbers and add an exponent to the variable totaling the number of variables in the equation:
Answer:
Example Question #331 : Algebraic Concepts
Multiply:
Multiply the whole numbers and add an exponent to the variable totaling the number of variables in the equation:
Answer:
Example Question #930 : Concepts
Solve for 
Certified Tutor
All HSPT Math Resources