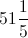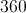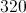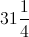We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

Create An Account

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Percentages

What percentage of is ?

Possible Answers:

$80\%$

$220\%$

$120\%$

$12\%$

$14\%$

Correct answer:

$120\%$

Explanation:

Rewrite the question in parts. A percentage is something out of $100\textup{ parts}$ .

$(\frac{x}{100})(10) = 12$

Solve for .

$(\frac{x}{10})= 12$

$x=120\%$

Report an Error

Example Question #581 : Concepts

128 is $40\%$ of what number?

Possible Answers:

360

300

320

$51 \frac{1}{5}$

$31\frac{1}{4}$

Correct answer:

320

Explanation:

128 is $40\%$ of a number we will call ; alternatively, 0.40 multiplied by is equal to 128 . Set up this equation and solve for :

0.4 N = 128

$0.4 N \div 0.4 = 128\div 0.4$

N= 320

Report an Error

Example Question #582 : Concepts

is what percent of 300 ?

Possible Answers:

$38 \frac{1}{2} \%$

$33 \%$

$33 \frac{1}{3} \%$

$25 \frac{2}{3} \%$

$37 \%$

Correct answer:

$25 \frac{2}{3} \%$

Explanation:

Set up the proportion statement, where is our answer, and solve:

$\frac{p}{100} = \frac{77}{300}$

$\frac{p}{100} \cdot 100 = \frac{77}{300} \cdot 100$

$p = \frac{77\cdot 100}{300} = \frac{77}{3} = 25 \frac{2}{3} \%$

Report an Error

Example Question #13 : Percentage

What is $60\%$ of ?

Possible Answers:

Correct answer:

Explanation:

One way to figure out what number is a percentage of a larger number is to convert the percent into a decimal and multiply it by the whole number. Since $60\%$ is equal to 0.60 , multiply this by .

$90 \times 0.60=54$

is your answer.

Report an Error

Example Question #31 : Percentage

$64\%$ of what number is 8,000 ?

Possible Answers:

12,500

15,000

16,000

12,800

14,400

Correct answer:

12,500

Explanation:

Taking 64% of a number is the same as multiplying that number by 0.64 . We can find our number, therefore, by dividing 8,000 by 0.64 :

$8,000 \div 0.64 = 12,500$

Report an Error

Example Question #12 : How To Find The Part From The Whole With Percentage

What is $125\%$ of 125 ?

Possible Answers:

137.5

150

156.25

132.5

100

Correct answer:

156.25

Explanation:

Rewrite $125\%$ as a decimal by writing 125 with a decimal point, then shifting it two spaces left:

$125.0\% = 1.25$

Multiply this by 125 :

$125 \times 1.25 = 156.25$

Report an Error

Example Question #583 : Concepts

Convert $23.2\%$ into a decimal.

Possible Answers:

2.32

0.232

232

0.0232

23.2

Correct answer:

0.232

Explanation:

In order to convert from a percentage to a decimal, simply remove the percentage and move the decimal place back two spaces or divide by 100.

$23.2\% = \frac{232}{100}= 0.232$

The decimal conversion is: 0.232

Report an Error

Example Question #4 : Use Proportional Relationships To Solve Multistep Ratio And Percent Problems: Ccss.Math.Content.7.Rp.A.3

What number increased by 25% is equal to 7?

Possible Answers:

$5\frac{5}{6}$

$5\frac{1}{4}$

$4\frac{2}{3}$

$5 \frac{3}{5}$

Correct answer:

$5 \frac{3}{5}$

Explanation:

To increase a number by 25% is to take

$(100 + 25) \% = 125 \%$ of the number, or, equivalently, multiply it by

$\frac{125}{100} = \frac{125 \div 25 }{100 \div 25 } = \frac{5}{4}$ .

Therefore, we divide 7 by $\frac{5}{4}$ :

$7 \div \frac{5}{4} = \frac{7 }{1}\div \frac{5}{4} = \frac{7 }{1}\times \frac{4} {5}= \frac{7\times 4 }{1\times 5} = \frac{28}{5}$

$28 \div 5 = 5 \textup{ R }3$ , so

$\frac{28}{5} = 5 \frac{3}{5}$ .

Report an Error

Example Question #5 : Use Proportional Relationships To Solve Multistep Ratio And Percent Problems: Ccss.Math.Content.7.Rp.A.3

What number decreased by 25% is equal to 7?

Possible Answers:

$9 \frac{1}{7}$

$8\frac{3}{4}$

$9 \frac{1}{3}$

$8\frac{2}{5}$

Correct answer:

$9 \frac{1}{3}$

Explanation:

To decrease a number by 25% is to take

$(100 - 25) \% = 75 \%$ of the number, or, equivalently, multiply it by

$\frac{75}{100} = \frac{75 \div 25 }{100 \div 25 } = \frac{3}{4}$ .

Therefore, we divide 7 by $\frac{3}{4}$ :

$7 \div \frac{3}{4} = \frac{7 }{1}\div \frac{3}{4} = \frac{7 }{1}\times \frac{4} {3}= \frac{7\times 4 }{1\times 3} = \frac{28}{3}$

$28 \div 3 = 9 \textup{ R }1$ , so

$\frac{28}{3} = 9 \frac{1}{3}$ .

Report an Error

Example Question #583 : Concepts

What is $3 \frac{1}{2}$ increased by 30%?

Possible Answers:

$3 \frac{4}{5}$

$4 \frac{1}{5}$

$4 \frac{11}{2 0}$

$3 \frac{13}{2 0}$

Correct answer:

$4 \frac{11}{2 0}$

Explanation:

Increasing a number by 30% is equivalent to taking 130% of a number, which in turn is equivalent to multiplying it by

$\frac{130}{100} = \frac{130 \div 10}{100 \div 10} = \frac{13}{10}$ .

$3 \frac{1}{2}$ increased by 30% is the product of $3 \frac{1}{2}$ and $\frac{13}{10}$ :

$3 \frac{1}{2} \times \frac{13}{10}$

$= \frac{3 \times 2 + 1}{2} \times \frac{13}{10}$

$= \frac{7}{2} \times \frac{13}{10}$

$= \frac{7 \times 13}{2 \times 10}$

$= \frac{91}{2 0}$

$91 \div 20 = 4 \textup{ R }11$ , so this quantity is equal to $4 \frac{11}{2 0}$ , the correct answer.

Report an Error

View Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

View Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View Tutors

Colton
Certified Tutor

Texas State University-San Marcos, Bachelor of Science, Mathematics.

All HSPT Math Resources

6 Diagnostic Tests 130 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

French Tutors in Denver, SSAT Tutors in Los Angeles, GMAT Tutors in Denver, MCAT Tutors in Dallas Fort Worth, ACT Tutors in Dallas Fort Worth, Spanish Tutors in Atlanta, LSAT Tutors in Boston, MCAT Tutors in Washington DC, GMAT Tutors in Houston, Algebra Tutors in Chicago

Popular Courses & Classes

GRE Courses & Classes in Denver, Spanish Courses & Classes in Philadelphia, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Boston, SSAT Courses & Classes in Houston, SAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Denver, SSAT Courses & Classes in Miami, SSAT Courses & Classes in Philadelphia

Popular Test Prep

SSAT Test Prep in Washington DC, ISEE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Los Angeles, LSAT Test Prep in Los Angeles, LSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Phoenix, ISEE Test Prep in Dallas Fort Worth, GRE Test Prep in Dallas Fort Worth, SSAT Test Prep in Atlanta, ACT Test Prep in Washington DC

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

HSPT Math : Concepts

Study concepts, example questions & explanations for HSPT Math

All HSPT Math Resources

Example Questions

Example Question #51 : Percentages

Example Question #581 : Concepts

Example Question #582 : Concepts

Example Question #13 : Percentage

Example Question #31 : Percentage

Example Question #12 : How To Find The Part From The Whole With Percentage

Example Question #583 : Concepts

Example Question #4 : Use Proportional Relationships To Solve Multistep Ratio And Percent Problems: Ccss.Math.Content.7.Rp.A.3

Example Question #5 : Use Proportional Relationships To Solve Multistep Ratio And Percent Problems: Ccss.Math.Content.7.Rp.A.3

Example Question #583 : Concepts

All HSPT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: