HiSET: Math : Measurement and Geometry
Study concepts, example questions & explanations for HiSET: Math
All HiSET: Math Resources
Example Questions
Example Question #1 : Apply Concepts Of Density In Modeling Situations
The graphic below shows a blueprint for a swimming pool.
If the pool is going to be 66 inches deep, how many cubic feet of water will it be able to hold? (1 ft = 12 in)
Notice that the outer dimensions of the blueprint are the dimensions for the entire pool, including the concrete, while the inner dimensions are for the part of the pool that will be filled with water. Therefore, we want to focus on just the inner dimensions.
Notice that the depth is given in inches, while the dimensions are in feet. Convert 66 inches to feet by dividing 66 by 12, since 12 inches makes a foot:
The inch units cancel out and leave us with just the feet units. 66 in is 5.5 ft.
Now we have all of the information we need to solve for the volume of the pool. The pool is a rectangular prism, and the formula for volume of a rectangular prism is
(In this case, the "height" of the swimming pool is its depth.)
The blueprint shows that the pool is 40 ft long and 30 ft wide. Plugging in the measurements from the problem, we get
Multiplying this out, we get 
Example Question #2 : Understand Right Triangles
Two of a triangle's interior angles measure 
A triangle that has interior angles of 
Since we know this triangle is a 30-60-90 triangle, we can use the special ratios that always hold true for this triangle's sides and angles to figure out the lengths of its other sides. The following ratio holds true for all 30-60-90 triangles, where the side in a fraction with a given angle is the side opposite that angle.
We're told that the hypotenuse of our triangle has a length of 
As you can see, for this particular triangle, 
Thus, the correct answer is 
Example Question #131 : Measurement And Geometry
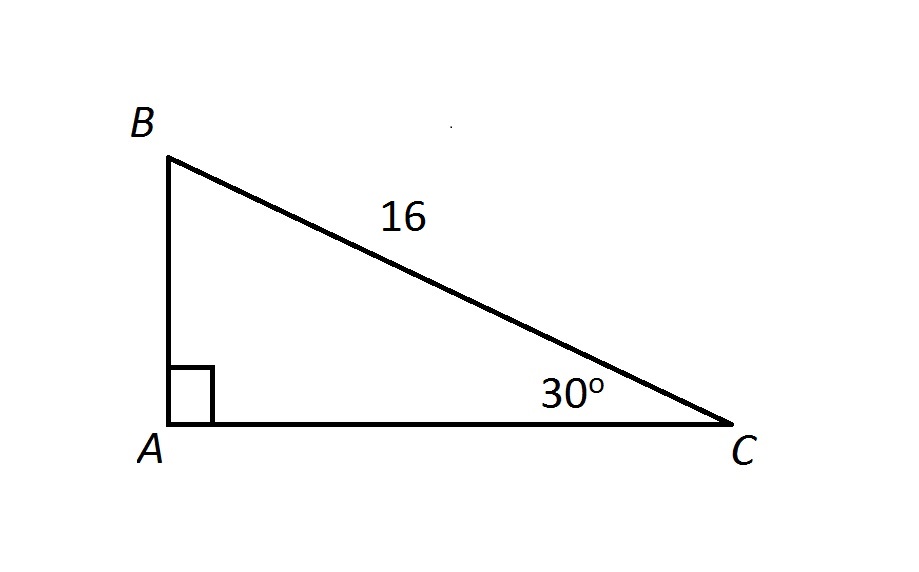
Examine the above triangle. Which of the following correctly gives the area of 
None of the other choices gives the correct response.
Since 
making 
By the 30-60-90 Triangle Theorem,
and
Refer to the diagram below:
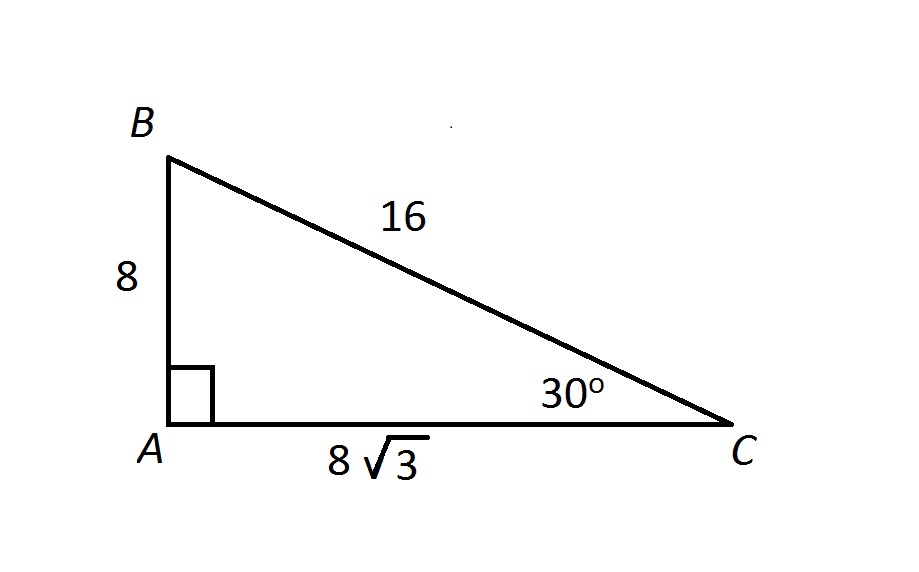
The area of a right triangle is equal to half the product of the lengths of its legs, so
the correct response.
Example Question #1 : Special Triangles
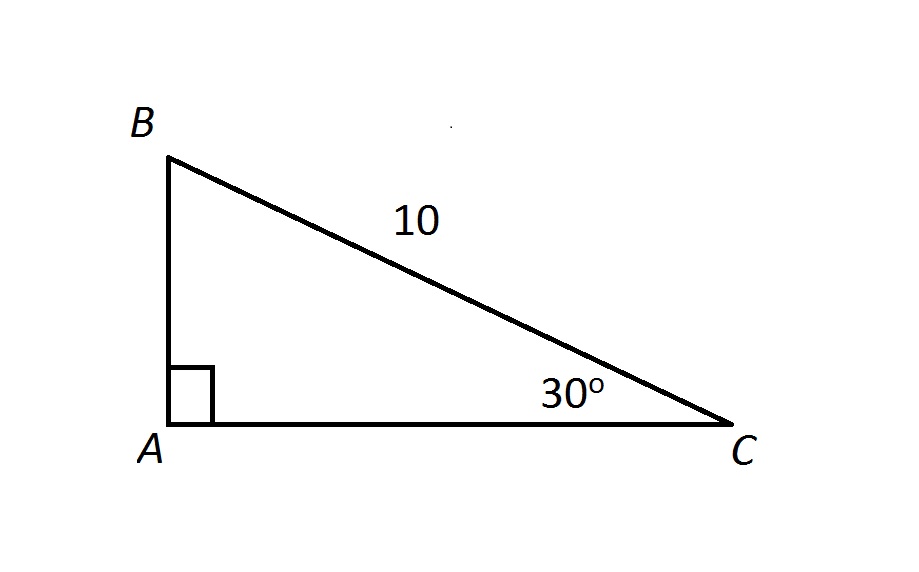
Examine the above triangle. Which of the following correctly gives the perimeter of 
Since 
making 
By the 30-60-90 Triangle Theorem,
and
Refer to the diagram below:
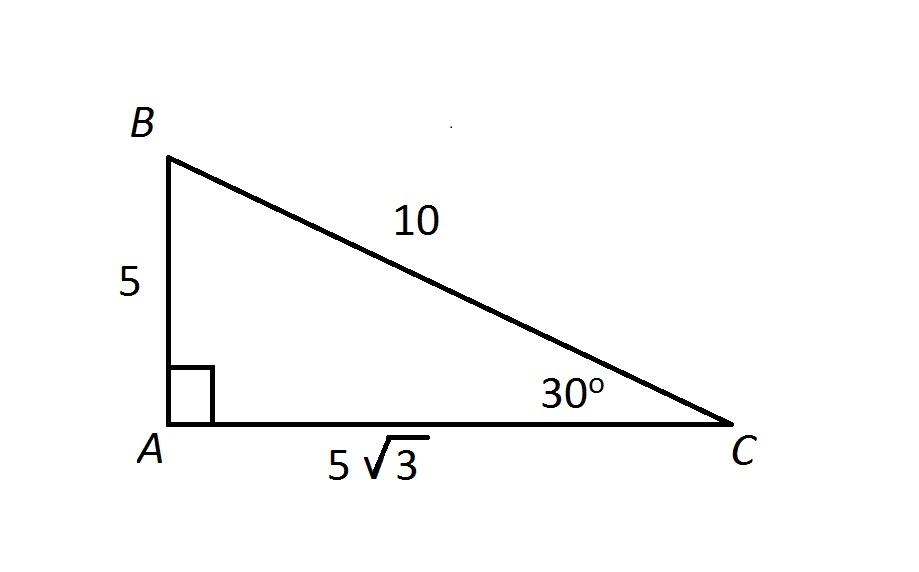
The perimeter - the sum of the sidelengths - is
All HiSET: Math Resources
