All HiSET: Math Resources
Example Questions
Example Question #1 : Functions And Function Notation
Define 

Evaluate 
The expression is undefined.
By definition,

so first, evaluate 



so evaluate 

the correct response.
Example Question #1 : Evaluate Functions For Inputs In Their Domains
Define functions 

Evaluate 
Undefined
By definition, 








the correct value.
Example Question #1 : Interpret Statements That Use Function Notation In Terms Of A Context
Consider the scenario below:
Helen is a painter. It takes her 3 days to make each painting. She has already made 6 paintings. Which of the following functions best models the number of paintings she will have after 
The question asks, "Which of the following functions best models the number of paintings she will have after 
From this, you know that the variable 

If it takes 3 days to make a painting, each day results in 

Additionally, she begins with 6 paintings. Therefore, even when zero days are spent working on paintings, she will have 6 paintings. In other words, 
As a result, the function will be
which can be rewritten as
Example Question #2 : Interpret Statements That Use Function Notation In Terms Of A Context
The daily pay in U.S. Dollars for a certain job is defined as the following function 

If an employee works for 7 hours in a day, how much is he or she paid?
The above function can be understood as, "An employee is paid $15 for each hour he or she works, plus a flat amount of $10."
If an employee works 7 hours, we can find the amount that he or she is paid by plugging in 7 for "Hours" in the equation:
Adhering to order of operations, we next find the product of 15 and 7:
Finally, we find the sum of 105 and 10:
The employee is paid $115.00 for seven hours' work.
Example Question #1 : Functions And Function Notation


Give the definition for 
By the two-point formula, the equation of a line through points 

where 

The first formula becomes
Since 


Isolate 
Replacing, the definition of 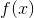

Example Question #6 : Functions And Function Notation
Define functions 
Give the domain of the composition 
None of the other choices gives the correct response.
The domain of the composition of functions 













Example Question #7 : Functions And Function Notation
Define functions 

Give the domain of the composition 
The domain of the composition of functions 














Therefore, we need to further restrict the domain to those values 

Equivalently,
Since 1 is positive, and the quotient is nonnegative as well, it follows that

and

The domain of 

Example Question #1 : Functions And Function Notation
Define functions 

Give the domain of the composition 
The domain of the composition of functions 











Therefore, the domain of 


Equivalently,
To solve this, first, solve the corresponding equation:
Factor the polynomial at left using the difference of squares pattern:
By the Zero Factor Property, either


or


These are the boundary values of the intervals to be tested. Choose an interior value of each interval and test it in the inequality:
Testing 

Testing 

Testing 

Include 


The correct domain is ![(-\infty, -4] \cup [4 , \infty)](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090725/gif.latex)
Example Question #9 : Functions And Function Notation
Define functions 

Give the domain of the composition 
The domain of the composition of functions 











The correct domain is 
Example Question #1 : Functions And Function Notation
Define functions 

Give the domain of the composition 
The domain of the composition of functions 
















that is,
Excluding this value from the domain, this leaves 

Certified Tutor
All HiSET: Math Resources










































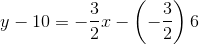







![\left ( - \infty, 0 \right ]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090645/gif.latex)








![[-4, 4 ]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090679/gif.latex)
![(-\infty, -4]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090680/gif.latex)
![(-\infty, -4] \cup [4 , \infty)](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090677/gif.latex)

















![[ -4,4]](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1090877/gif.latex)












