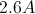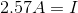In series, the equivalent resistance is equal to the sum of each individual resistance. In parallel, the inverse of equivalent resistance is equal to the sum of the inverses of each individual resistance.

We can calculate these two values, and then find the difference between them.

Find the difference:

When working in a series, the total resistance is the sum of the individual resistances.

Use the given values for each individual resistor to solve for the total resistance.

The formula for resistance in parallel is:

We are given the values for each individual resistor, allowing us to solve for the total resistance.

In series, there are no branches for the current to travel down.  Therefore it is like a one lane highway so the current is the same throughout the entire circuit.

Consider a set of parallel resistors that are connected to the battery.  Each resistor is on its own loop to the battery.  Therefore each resistor has its own potential difference that is equal to the battery.  That is why if one bulb goes out in a parallel circuit, the other stays lit.  Each resistor has its own connection independent of the others in the circuit.

Think of resistors as doors, preventing the flow of people (electrons). Imagine the following scenarios: a large group of people are in a room and all try to leave at once. If the five resistors are in series, that's like having all of these people trying to go through all five doors before they can leave. In a circuit, all the electrons in the current must pass through every resistor.

If the resistors are in parallel, it's like having five separate doors from the room. All of a sudden, the group can leave MUCH faster, encountering less resistance to their flow out of the room. The path of the electrons can split, allowing each particle to pass through only one resistor.

From a formula perspective, the resistors in series are simply summed together to find the equivalent resistance.

In parallel, however, the reciprocals are summed to find the reciprocal equivalent resistance.

Adding whole numbers will always give you a much greater result than adding fractions. For the exact same set of resistors, arrangement in series will have a greater total resistance than arrangement in parallel.

To find the net resistance of the circuit, we must summarize all of the different resistors, one piece at a time.  To begin, let’s start with the two resistors in the upper left had corner which are in series.  In series resistance can be added together.  We can replace these two resistors with a single resistor that is valued at .

Next, this new resistor is in parallel with the resistor that is on the diagonal line from point A to point B.  In parallel we can add resistors through the equation 

This new resistor is now in series with the resistor that is between points B & C.  In series we can just add these resistors up.

This new resistor is now in parallel with the resistor that is between points A & C.  In parallel we can add resistors through the equation 

This new resistor is now in series with the resistor that is between the battery and point C.  In series we can just add these resistors up.

To begin, let us start with the  resistor and the  resistor that are in parallel. In parallel we can add resistors through the equation 

This new resistor is now in series with the two  resistors.  In series we can just add these resistors up.

This new resistor is now in parallel with the  resistor. In parallel we can add resistors through the equation 

This new resistor is now in series with the  and  resistor.  In series we can just add these resistors up.

For this problem, use Ohm's law: .

We are given the voltage and the resistance. Using these terms, we can solve for the current.

For this problem, use Ohm's law: .

We are given the current and the resistance. Using these terms, we can solve for the voltage.