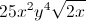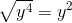We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Understanding Square Roots

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Radicals

Simplify the expression. Find the positive solution only.

$\sqrt{50x^3y^4}$ $\displaystyle \sqrt{50x^3y^4}$

Possible Answers:

$25x^2y^4\sqrt{2x}$ $\displaystyle 25x^2y^4\sqrt{2x}$

$5xy^2\sqrt{2x}$ $\displaystyle 5xy^2\sqrt{2x}$

$5xy\sqrt{2x}$ $\displaystyle 5xy\sqrt{2x}$

25xy $\displaystyle 25xy$

$xy^2\sqrt{50xy^2}$ $\displaystyle xy^2\sqrt{50xy^2}$

Correct answer:

$5xy^2\sqrt{2x}$ $\displaystyle 5xy^2\sqrt{2x}$

Explanation:

When working in square roots, each component can be treated separately.

$\sqrt{50x^3y^4}=\sqrt{50}\sqrt{x^3}\sqrt{y^4}$ $\displaystyle \sqrt{50x^3y^4}=\sqrt{50}\sqrt{x^3}\sqrt{y^4}$

Now, we can simplify each term.

$\sqrt{50}=5\sqrt{2}$ $\displaystyle \sqrt{50}=5\sqrt{2}$

$\sqrt{x^3}=x\sqrt{x}$ $\displaystyle \sqrt{x^3}=x\sqrt{x}$

$\sqrt{y^4}=y^2$ $\displaystyle \sqrt{y^4}=y^2$

Combine the simplified terms to find the answer. Anything outside of the square root is combined, while anything under the root is combined under the root.

$(5\sqrt{2})(x\sqrt{x})(y^2)=5xy^2\sqrt{2x}$ $\displaystyle (5\sqrt{2})(x\sqrt{x})(y^2)=5xy^2\sqrt{2x}$

Report an Error

View Tutors

Joel
Certified Tutor

Montana State University, Bachelor in Arts, Economics. Montana State University - Bozeman, Bachelor, Psychology.

View Tutors

Nicole
Certified Tutor

Caldwell University, Bachelor, Education and English. Caldwell University, Master's/Graduate, Education.

View Tutors

Desha-Soleil
Certified Tutor

McMaster University, Bachelor of Science, Political Science and Government.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Houston, Biology Tutors in Washington DC, ACT Tutors in Boston, Biology Tutors in Seattle, Algebra Tutors in Washington DC, Biology Tutors in Dallas Fort Worth, Math Tutors in Atlanta, GMAT Tutors in San Diego, French Tutors in Chicago, ISEE Tutors in Seattle

Popular Courses & Classes

Spanish Courses & Classes in Miami, SSAT Courses & Classes in Houston, GMAT Courses & Classes in Denver, SSAT Courses & Classes in Dallas Fort Worth, SAT Courses & Classes in Denver, SAT Courses & Classes in Los Angeles, SAT Courses & Classes in Seattle, MCAT Courses & Classes in Atlanta, LSAT Courses & Classes in Washington DC, Spanish Courses & Classes in San Francisco-Bay Area

Popular Test Prep

ISEE Test Prep in Los Angeles, ISEE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Miami, GMAT Test Prep in San Diego, MCAT Test Prep in Los Angeles, ISEE Test Prep in Boston, MCAT Test Prep in Miami, GMAT Test Prep in Houston, SAT Test Prep in Miami, GMAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Understanding Square Roots

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Understanding Radicals

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: