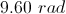Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Understanding Radians and Conversions

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #61 : Trigonometry

If angle equals $136^{\circ}$ , what is the equivalent angle in radians (to the nearest hundredth)?

Possible Answers:

$1.18\ rad$

$136\ rad$

$2.37\ rad$

$7.79\ rad$

$23.7\ rad$

Correct answer:

$2.37\ rad$

Explanation:

To convert between radians and degrees, it is important to remember that:

$\pi\, rad = 180^{\circ}$

With this relationship in mind, we can convert from degrees to radians with the following formula:

$136^{\circ}\cdot \frac{\pi}{180^{\circ}} = 2.37\,rad$

Report an Error

Example Question #62 : Trigonometry

If $\angle A$ equals $45^{\circ}$ , what is the equivalent angle in radians (to the nearest hundredth)?

Possible Answers:

$0.56\ rad$

$0.79\ rad$

$3.14\ rad$

$4.71\ rad$

$1.57\ rad$

Correct answer:

$0.79\ rad$

Explanation:

To convert between radians and degrees, it is important to remember that:

$\pi\, rad = 180^{\circ}$

With this relationship in mind, we can convert from degrees to radians with the following formula:

$45^{\circ}\cdot \frac{\pi}{180^{\circ}} = 0.79\,rad$

Report an Error

Example Question #63 : Trigonometry

If $\angle B$ is $275^{\circ}$ , what is the equivalent angle in radians (to the nearest hundredth)?

Possible Answers:

$3.27\ rad$

$2.40\ rad$

$4.80\ rad$

$9.60\ rad$

$1.37\ rad$

Correct answer:

$4.80\ rad$

Explanation:

To convert between radians and degrees, it is important to remember that:

$\pi\, rad = 180^{\circ}$

With this relationship in mind, we can convert from degrees to radians with the following formula:

$275^{\circ}\cdot \frac{\pi}{180^{\circ}} = 4.80\,rad$

Report an Error

Example Question #64 : Trigonometry

If an angle is $98^{\circ}$ , what is the equivalent angle in radians (to the nearest hundredth)?

Possible Answers:

$3.14\ rad$

$0.86\ rad$

$3.42\ rad$

$1.27\ rad$

$1.71\ rad$

Correct answer:

$1.71\ rad$

Explanation:

To convert between radians and degrees, it is important to remember that:

$\pi\, rad = 180^{\circ}$

With this relationship in mind, we can convert from degrees to radians with the following formula:

$98^{\circ}\cdot \frac{\pi}{180^{\circ}}= 1.71\,rad$

Report an Error

Example Question #65 : Trigonometry

What angle below is equivalent to $90^{\circ}$ ?

Possible Answers:

$4\pi\,radians$

$\frac{\pi}{4}\,radians$

$\pi\,radians$

$\frac{\pi}{2}\,radians$

$2\pi\,radians$

Correct answer:

$\frac{\pi}{2}\,radians$

Explanation:

To convert between radians and degrees, it is important to remember that:

$\pi\, radians = 180\, degrees$

With this relationship in mind, we can convert from degrees to radians with the following formula:

$90^{\circ}\cdot \frac{\pi}{180^{\circ}} = \frac{1}{2}\cdot \pi = \frac{\pi}{2}\,radians$

Report an Error

Example Question #31 : Understanding Radians And Conversions

If an angle is 2.43 radians, what is the equivalent angle in degrees?

Possible Answers:

$145^{\circ}$

$45^{\circ}$

$127^{\circ}$

$90^{\circ}$

$139.23^{\circ}$

Correct answer:

$139.23^{\circ}$

Explanation:

To answer this question, it is important to remember the relationship:

$\pi\,radians = 180\,degrees$

From here, we can set up the following formula:

$2.43\,rad\cdot \frac{180^\circ}{\pi\,rad} = 139.23^{\circ}$

Multiplying across, we see that the units of radians cancel out and we are left with units in degrees.

Report an Error

Example Question #32 : Understanding Radians And Conversions

If an angle equals 5.75 radians, what is the equivalent angle in degrees?

Possible Answers:

$360^{\circ}$

$180^{\circ}$

$90^{\circ}$

$329.45^{\circ}$

$3.14^{\circ}$

Correct answer:

$329.45^{\circ}$

Explanation:

To answer this question, it is important to remember the relationship:

$\pi\,radians = 180\,degrees$

From here, we can set up the following formula:

$5.75\,rad\cdot \frac{180^\circ}{\pi\,rad} = 329.45^{\circ}$

Multiplying across, we see that the units of radians cancel out and we are left with units in degrees.

Report an Error

Example Question #33 : Understanding Radians And Conversions

If an angle equals 15.71 radians, what is the equivalent angle in degrees?

Possible Answers:

$3.14^{\circ}$

$670^{\circ}$

$900^{\circ}$

$45^{\circ}$

$1.57^{\circ}$

Correct answer:

$900^{\circ}$

Explanation:

To answer this question, it is important to remember the relationship:

$\pi\,radians = 180\,degrees$

From here, we can set up the following formula:

$15.71\,rad\cdot \frac{180^\circ}{\pi\,rads} = 900^{\circ}$

Multiplying across, we see that the units of radians cancel out and we are left with units in degrees.

Report an Error

Example Question #34 : Understanding Radians And Conversions

If an angle equals 6.4 radians, what is the equivalent angle in degrees?

Possible Answers:

$360^{\circ}$

$31.4^{\circ}$

$180^{\circ}$

$366.69^{\circ}$

$5.78^{\circ}$

Correct answer:

$366.69^{\circ}$

Explanation:

To answer this question, it is important to remember the relationship:

$\pi\,radians = 180\,degrees$

From here, we can set up the following formula:

$6.4\,rad\cdot \frac{180^\circ}{\pi\,rads}= 366.69^{\circ}$

Multiplying across, we see that the units of radians cancel out and we are left with units in degrees.

Report an Error

Example Question #35 : Understanding Radians And Conversions

If an angle is 3.55 radians, what is the equivalent angle in degrees?

Possible Answers:

$270.45^{\circ}$

$360^{\circ}$

$203.40^{\circ}$

$146.87^{\circ}$

$200^{\circ}$

Correct answer:

$203.40^{\circ}$

Explanation:

To answer this question, it is important to remember the relationship:

$\pi\,radians = 180\,degrees$

From here, we can set up the following formula:

$3.55\,rad\cdot \frac{180^\circ}{\pi\,rad} = 203.40^{\circ}$

Multiplying across, we see that the units of radians cancel out and we are left with units in degrees.

Report an Error

View Tutors

Donald
Certified Tutor

Cleveland State University, Bachelor of Science, Chemistry. University of Southern California, Doctor of Philosophy, Organic ...

View Tutors

Victoria
Certified Tutor

Norte Dame de Namur University, Bachelor in Arts, Sociology. University of San Francisco, Master of Arts, Organizational Lead...

View Tutors

Shweta
Certified Tutor

All India Management Association , Master's/Graduate, Human Resource Management . Indian Law Institute , Master's/Graduate, C...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Washington DC, Spanish Tutors in Los Angeles, ISEE Tutors in Dallas Fort Worth, GRE Tutors in San Francisco-Bay Area, MCAT Tutors in New York City, GMAT Tutors in Dallas Fort Worth, Chemistry Tutors in Atlanta, Math Tutors in Washington DC, Reading Tutors in Los Angeles, GRE Tutors in New York City

Popular Courses & Classes

LSAT Courses & Classes in Seattle, GRE Courses & Classes in Atlanta, ACT Courses & Classes in Boston, ISEE Courses & Classes in Houston, MCAT Courses & Classes in Chicago, ACT Courses & Classes in Philadelphia, SSAT Courses & Classes in Philadelphia, SAT Courses & Classes in San Diego, ACT Courses & Classes in Houston, ACT Courses & Classes in Atlanta

Popular Test Prep

ACT Test Prep in Philadelphia, LSAT Test Prep in New York City, ACT Test Prep in Boston, MCAT Test Prep in Chicago, ACT Test Prep in Houston, ACT Test Prep in Atlanta, SAT Test Prep in Houston, ISEE Test Prep in Washington DC, SAT Test Prep in Miami, SSAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Understanding Radians and Conversions

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #61 : Trigonometry

Example Question #62 : Trigonometry

Example Question #63 : Trigonometry

Example Question #64 : Trigonometry

Example Question #65 : Trigonometry

Example Question #31 : Understanding Radians And Conversions

Example Question #32 : Understanding Radians And Conversions

Example Question #33 : Understanding Radians And Conversions

Example Question #34 : Understanding Radians And Conversions

Example Question #35 : Understanding Radians And Conversions

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: