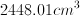Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Cubes

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #651 : Geometry

The side of a cube has a length of $\dpi{100} \small 5 cm$ . What is the total surface area of the cube?

Possible Answers:

$\dpi{100} \small 150cm^{2}$

$\dpi{100} \small 25 cm^{2}$

$\dpi{100} \small 5cm^{2}$

$\dpi{100} \small 50 cm^{2}$

$\dpi{100} \small 125 cm^{2}$

Correct answer:

$\dpi{100} \small 150cm^{2}$

Explanation:

A cube has 6 faces. The area of each face is found by squaring the length of the side.

$\dpi{100} \small 5\times 5 = 25$

Multiply the area of one face by the number of faces to get the total surface area of the cube.

$\dpi{100} \small 25 \times 6=150$

Report an Error

Example Question #21 : Cubes

What is the surface area of a cube if its height is 3 cm?

Possible Answers:

$63\ cm^2$

$36\ cm^2$

$45\ cm^2$

$54\ cm^2$

$25\ cm^2$

Correct answer:

$54\ cm^2$

Explanation:

The area of one face is given by the length of a side squared.

$A_{face}=(3cm)^2=9\ cm^2$

The area of 6 faces is then given by six times the area of one face: 54 cm².

$A_{total}=6(A_{face})=6(9\ cm^2)=54\ cm^2$

Report an Error

Example Question #3 : How To Find The Surface Area Of A Cube

A sphere with a volume of $\frac{32}{3}$ $\pi m^{3}$ is inscribed in a cube, as shown in the diagram below.

Act4

What is the surface area of the cube, in $m^{2}$ ?

Possible Answers:

$48\pi ^{2}\ m^{2}$

$96\ m^{2}$

$48\pi \ m^{2}$

$24\ m^{2}$

$48\ m^{2}$

Correct answer:

$96\ m^{2}$

Explanation:

We must first find the radius of the sphere in order to solve this problem. Since we already know the volume, we will use the volume formula to do this.

$V_{sphere}=\frac{4}{3}\pi r^{3}$

$\frac{32}{3}\pi =\frac{4}{3}\pi r^{3}$

$\frac{32}{3}=\frac{4}{3}r^{3}$

$\frac{3}{4}\cdot \frac{32}{3}= r^{3}$

$8=r^{3}$

r=2

With the radius of the sphere in hand, we can now apply it to the cube. The radius of the sphere is half the distance from the top to the bottom of the cube (or half the distance from one side to another). Therefore, the radius represents half of a side length of a square. So in this case

$side=2\cdot 2=4$

The formula for the surface area of a cube is:

$SA_{cube}=6s^{2}$

$6s^{2}=6\cdot (4)^{2}=6\cdot 16=96$

The surface area of the cube is $96\ m^{2}$

Report an Error

Example Question #22 : Cubes

If a right triangle has a hypotenuse of length 5, and the length of the other sides are and , what would be the surface area of a cube having side length ?

Possible Answers:

$5\sqrt{5}$

None of these answers.

$25\sqrt{5}$

Correct answer:

Explanation:

By the Pythagorean Theorem,

x^2 + (2x)^2 = 5^2

x^2 + 4x^2 = 25

5x^2 = 25

x^2 = 5

$x=\sqrt{5}$

The surface area of a cube having 6 sides, is 6 times the area of one of its sides.

The area of any side of a cube is the square of the side length.

So if the side length is , the area of any side is x^2 , or .

Thus the surface area of the cube is

6*(5)

=30

Report an Error

Example Question #1 : How To Find The Volume Of A Cube

A box measures $11 \ cm \times 10 \ cm \times 8 \ cm$ . How many dice can fit in this box if the dice are cubes with sides of length $2 \ cm$ ?

Possible Answers:

100 dice

880 dice

110 dice

dice

800 dice

Correct answer:

100 dice

Explanation:

Since the dice are $2 \ cm$ on each of their sides, of them would measure $10 \ cm$ in length when standing face-to-face. This means dice will fit along the edge of the box that measures $10 \ cm$ .

dice will also fit on the edge of the box measuring $11 \ cm$ , but will not fit since adding an additional die would bring the length of the dice standing face-to-face up to $12 \ cm$ . There are no half-dice to fill the gap, so there is a small empty space on this side.

dice will fit along the side that measures $8 \ cm$ .

Treating "dice" as the unit of measurement instead of and considering only the volume where the dice will fit, one ends up with a rectangular shape measuring dice $\times$ dice $\times$ dice. The volume of this shape is the number of dice that will fit in this area (and thus the box). Find the volume by multiplying all lengths of the shape's sides together:

$5 \times 5 \times 4$ dice = 100 dice.

Report an Error

Example Question #2 : How To Find The Volume Of A Cube

What is the volume of a cube with a side length of 7?

Possible Answers:

300

343

Correct answer:

343

Explanation:

When searching for the volume of a cube we are looking for the amount of the space enclosed by the cube.

To find this we must know the formula for the volume of a cube which is $Volume\: of\: Cube=s^{3}$

Using this formula we plug in the side length for to get $V=7^{3}$

Cube the side length to arrive at the answer of $7^{3}=343$

The answer is 343 .

Report an Error

Example Question #3 : How To Find The Volume Of A Cube

If the volume of a cube is 3375, what is the length of each side?

Possible Answers:

843.75

Correct answer:

Explanation:

To find this we must know the formula for the volume of a cube which is

We plug the volume into the equation yielding $3375= s^{3}$

Then we take the cube root of both sides giving us $\sqrt[3]{3375}=\sqrt[3]{s^{3}}$

We now know 15=s

The answer is .

Report an Error

Example Question #22 : Cubes

What is the sum of the number of vertices, edges, and faces of a cube?

Possible Answers:

None of the answers are correct

Correct answer:

Explanation:

Vertices = three planes coming together at a point = 8

Edges = two planes coming together to form a line = 12

Faces = one plane as the surface of the solid = 6

Vertices + Edges + Faces = 8 + 12 + 6 = 26

Report an Error

Example Question #4 : How To Find The Volume Of A Cube

What is the volume, in centimeters, of a rectangular prism with a length of l=2.4cm , a width of w=255mm , and a height of h=0.44m ?

Possible Answers:

$2692.8cm^{3}$

$2448.01cm^{3}$

$\dpi{100}269.28 cm^{3}$

$26928cm^{3}$

$\dpi{100} 2962.8cm^{3}$

Correct answer:

$2692.8cm^{3}$

Explanation:

In order to solve this problem, we need to make sure that the measurements given are in uniform units. In this case, we will use centimeters; therefore, we need to convert the other units of meters and millimeters into centimeters via dimensional analysis.

Solve for the width.

$w=\frac{255mm}{1}*\frac{1cm}{10mm}$

w=25.5cm

Solve for the height.

$h=\frac{0.44m}{1}*\frac{100cm}{1m}$

h=44cm

Now, solve for volume by using the formula V=l*w*h .

V=2.4cm*25.5cm*44cm

$\rightarrow 2692.8cm^{3}$

If you calculated $\dpi{100}269.28 cm^{3}$ , then you did not convert into appropriate units.

Report an Error

Example Question #5 : How To Find The Volume Of A Cube

Square_with_diagonal What is the volume of a cube with a diagonal one one of its faces of $\dpi{100} d=6.27ft$ ?

Possible Answers:

$78.51ft^{3}$

Not enough information to solve

$264.50ft^{3}$

$246.50ft^{3}$

$87.15ft^{3}$

Correct answer:

$87.15ft^{3}$

Explanation:

A few facts need to be known to solve this problem. Observe that the diagonal of the square face of the cube cuts the qradilateral into two right isosceles triangles; therefore, the length of a side of the square to its diagonal is the same as an isosceles right triangle's leg to its hypotenuse: $1:\sqrt{2}$ .

$\frac{s}{d}=\frac{1}{\sqrt{2}}$

$\dpi{100} \dpi{100} \dpi{100} \frac{s}{6.27ft}=\frac{1}{\sqrt{2}}$

Rearrange an solve for .

$\dpi{100} \dpi{100} s=\frac{6.27ft}{\sqrt{2}}$

Now, solve for the volume.

$V=s^{3}$

$V=(\frac{6.27ft}{\sqrt{2}})*(\frac{6.27ft}{\sqrt{2}})*(\frac{6.27ft}{\sqrt{2}})$

$V=\frac{246.491883ft^{3}}{2\sqrt{2}}$

$\rightarrow87.15ft^{3}$

Report an Error

View Tutors

Donald
Certified Tutor

Cleveland State University, Bachelor of Science, Chemistry. University of Southern California, Doctor of Philosophy, Organic ...

View Tutors

Victoria
Certified Tutor

Norte Dame de Namur University, Bachelor in Arts, Sociology. University of San Francisco, Master of Arts, Organizational Lead...

View Tutors

Shweta
Certified Tutor

All India Management Association , Master's/Graduate, Human Resource Management . Indian Law Institute , Master's/Graduate, C...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Boston, GMAT Tutors in Atlanta, MCAT Tutors in Washington DC, Biology Tutors in Denver, English Tutors in Dallas Fort Worth, Statistics Tutors in Los Angeles, SAT Tutors in San Francisco-Bay Area, GMAT Tutors in New York City, Calculus Tutors in New York City, SSAT Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in New York City, SAT Courses & Classes in Miami, GRE Courses & Classes in Houston, ISEE Courses & Classes in Phoenix, SAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Phoenix, SAT Courses & Classes in Chicago, SSAT Courses & Classes in Seattle, ACT Courses & Classes in Chicago

Popular Test Prep

GRE Test Prep in Miami, MCAT Test Prep in Seattle, ISEE Test Prep in San Diego, SAT Test Prep in Dallas Fort Worth, MCAT Test Prep in Phoenix, SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in San Francisco-Bay Area, GRE Test Prep in Philadelphia, MCAT Test Prep in Houston, MCAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Cubes

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #651 : Geometry

Example Question #21 : Cubes

Example Question #3 : How To Find The Surface Area Of A Cube

Example Question #22 : Cubes

Example Question #1 : How To Find The Volume Of A Cube

Example Question #2 : How To Find The Volume Of A Cube

Example Question #3 : How To Find The Volume Of A Cube

Example Question #22 : Cubes

Example Question #4 : How To Find The Volume Of A Cube

Example Question #5 : How To Find The Volume Of A Cube

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: