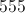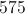We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : How to find the surface area of a pyramid

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Pyramids

What is the surface are of a pyramid with a square base length of 15 and a slant height (the height from the midpoint of one of the side lengths to the top of the pyramid) of 12?

Possible Answers:

575

585

565

555

Correct answer:

585

Explanation:

To find the surface area of a pyramid we must add the areas of all five of the shapes creating the pyramid together.

We have four triangles that all have the same area and a square that supports the pyramid.

To find the area of the square we take the side length of 15 and square it $15^{2}=225$

The area of the square is 225 .

To find the area of the triangle we must use the equation for the area of a triangle which is $\frac{base\times height}{2}$

Plug in the slant height 12 as the height of the triangle and use the side length of the square 15 as the base in our equation to get

$\frac{1}{2}*15*12=90$

The area of each triangle is .

We then multiply the area of each triangle by 4 to find the area of all four triangles 4*90=360 .

The four triangles have a surface area of 360 .

We add the surface area of the four triangles with the area of the square to get the answer for the surface area of the pyramid which is 360+225=585 .

The answer is 585 .

Report an Error

Example Question #75 : Solid Geometry

Find the surface area of the following pyramid.

Pyramid

Possible Answers:

330m^2

320m^2

340m^2

360m^2

350m^2

Correct answer:

340m^2

Explanation:

The formula for the surface area of a pyramid is:

$SA = 4 \left(A_{triangle}\right)+Base$

$SA = 4 \left(\frac{1}{2}{h_{s}}w\right)+(lw)$

Where h_s is the length of the slant height, is the width of the base, and is the length of the base

In order to determine the areas of the triangle, you will need to use the Pythagorean Theorem to find the slant height:

A^2 + B^2 = C^2

A^2 + (5m)^2 = (13m)^2

A^2 = 144m^2

A = 12m

Plugging in our values, we get:

$SA = 4 \left(\frac{1}{2}\cdot (12m)(10m)\right)+((10m)(10m))$

SA = 240m^2+100m^2 = 340m^2

Report an Error

Example Question #75 : Solid Geometry

Find the surface area of the following pyramid.

Pyramid

Possible Answers:

326m^2

316m^2

356m^2

336m^2

346m^2

Correct answer:

336m^2

Explanation:

The formula for the surface area of a pyramid is:

$SA = (base)+\frac{1}{2}(perimeter)(slant height)$

$SA = (l)(w) + \frac{1}{2}(l+l+w+w)(h_s)$

Where is the length of the base, is the width of the base, and h_s is the slant height

Use the Pythagorean Theorem to find the length of the slant height:

A^2 + B^2 = C^2

A^2 + (6m)^2 = (10m)^2

A = 8m

Plugging in our values, we get:

$SA = (12m)(12m) + \frac{1}{2}(12m+12m+12m+12m)(8m)$

SA = 336m^2

Report an Error

Example Question #1 : Pyramids

What is the surface area of a square pyramid with a base side equal to 4 and a slant length equal to 6?

Possible Answers:

Correct answer:

Explanation:

The surface area of of a square pyramid can be determined using the following equation:

SA=2bs+b^2

SA=(2)(6)(4)+4^2

SA=48+16=64

Report an Error

Example Question #1 : How To Find The Surface Area Of A Pyramid

What is the surface area of a square pyramid with a height of 12 in and a base side length of 10 in?

Possible Answers:

$360 \textup{ in}^{2}$

$420 \textup{ in}^{2}$

$150 \textup{ in}^{2}$

$100 \textup{ in}^{2}$

$260 \textup{ in}^{2}$

Correct answer:

$360 \textup{ in}^{2}$

Explanation:

The surface area of a square pyramid can be broken into the area of the square base and the areas of the four triangluar sides. The area of a square is given by:

$A = s^{2} = 100 in^{2}$

The area of a triangle is:

$A = \frac{1}{2} bh$

The given height of 12 in is from the vertex to the center of the base. We need to calculate the slant height of the triangular face by using the Pythagorean Theorem:

$SH^{2} = H^{2} + B^{2}$

where H=12 and B= 5 (half the base side) resulting in a slant height of 13 in.

So, the area of the triangle is:

$A = \frac{1}{2} bh = \frac{1}{2} \cdot 10 \cdot 13 = 65 in^{2}$

There are four triangular sides totaling $260 in^{2}$ for the sides.

The total surface area is thus $360 in^{2}$ , including all four sides and the base.

Report an Error

View Tutors

Amir
Certified Tutor

University of Mississippi, Master of Science, Structural Engineering. University of South Florida-Main Campus, Doctor of Scie...

View Tutors

Dawn
Certified Tutor

University of Oregon, Bachelor in Arts, Biochemistry and Molecular Biology. Johns Hopkins University, Doctor of Philosophy, E...

View Tutors

Abhisek
Certified Tutor

University of Florida, Bachelor of Engineering, Computer Science.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Physics Tutors in Philadelphia, Biology Tutors in Los Angeles, English Tutors in Chicago, Physics Tutors in Dallas Fort Worth, Chemistry Tutors in Atlanta, Math Tutors in Dallas Fort Worth, Physics Tutors in Atlanta, GRE Tutors in Miami, SAT Tutors in San Francisco-Bay Area, Physics Tutors in New York City

Popular Courses & Classes

GMAT Courses & Classes in Houston, GRE Courses & Classes in New York City, Spanish Courses & Classes in Seattle, LSAT Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Miami, LSAT Courses & Classes in Seattle, SSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Boston, LSAT Courses & Classes in Phoenix, GRE Courses & Classes in Dallas Fort Worth

Popular Test Prep

LSAT Test Prep in San Diego, ISEE Test Prep in Washington DC, GRE Test Prep in San Francisco-Bay Area, SSAT Test Prep in Philadelphia, MCAT Test Prep in Atlanta, SSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Phoenix, GRE Test Prep in Philadelphia, SSAT Test Prep in San Diego, GRE Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : How to find the surface area of a pyramid

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Pyramids

Example Question #75 : Solid Geometry

Example Question #75 : Solid Geometry

Example Question #1 : Pyramids

Example Question #1 : How To Find The Surface Area Of A Pyramid

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: