All High School Math Resources
Example Questions
Example Question #31 : Mathematical Relationships And Basic Graphs
Simplify the following complex number expression:
Begin by multiplying the numerator and denominator by the conjugate of the denominator:
Combine like terms:
Simplify. Remember that 

Example Question #41 : Algebra Ii
Simplify the following expression:
Simplifying expressions with complex numbers uses exactly the same process as simplifying expressings with one variable. In this case, 
Example Question #41 : Algebra Ii
Simplify the following complex number expression:
Use the FOIL (First, Outer, Inner, Last) method to expand the expression:
Simplify. Remember that 

Example Question #41 : Mathematical Relationships And Basic Graphs
Simplify the expression. Find the positive solution only.
When working in square roots, each component can be treated separately.
Now, we can simplify each term.
Combine the simplified terms to find the answer. Anything outside of the square root is combined, while anything under the root is combined under the root.
Example Question #1241 : High School Math
Convert the radical to exponential notation.
Remember that any term outside the radical will be in the denominator of the exponent.
Since 
Example Question #1242 : High School Math
What is the value of 
243
2.41
9
27
3
243
An exponent written as a fraction can be rewritten using roots. 
![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92839/gif.latex)
![\sqrt[2]{9^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121574/gif.latex)
![(\sqrt[2]{9})^{5}=3^{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/92840/gif.latex)
Example Question #2 : Understanding Radicals
Express the following radical in rational (exponential) form:
To convert the radical to exponent form, begin by converting the integer:

Now, divide each exponent by 
Finally, simplify the exponents:
Example Question #1 : Understanding Radicals
Express the following radical in rational (exponential) form:
To convert the radical to exponent form, begin by converting the integer:
Now, divide each exponent by 
Finally, simplify the exponents:
Example Question #2 : Radicals
Which fraction is equivalent to 
Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Example Question #1243 : High School Math
Simplify the following radical. Express in rational (exponential) form.
Multiply the numerator and denominator by the compliment of the denominator:
Simplify the expression:
Certified Tutor
All High School Math Resources

































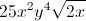






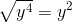

![\small \sqrt[4]{13}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/116532/gif.latex)




![\sqrt[b]{x^a}=x^{\frac{a}{b}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88790/gif.latex)
![\sqrt[4]{13}=13^{\frac{1}{4}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88791/gif.latex)









![\sqrt[4]{96a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152426/gif.latex)





![\sqrt[4]{96a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152427/gif.latex)
![=\sqrt[4]{3\cdot 2^5a^5b^7c^8}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/152734/gif.latex)
















