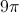We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Solid Geometry

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #5 : How To Find The Volume Of A Cylinder

Cylinder_with_a_sphere

A sphere with a radius of r=2cm is circumscribed in a cylinder. What is the cylinder's volume?

Possible Answers:

$27.28cm^{3}$

Not enough information to solve

$\dpi{100} 28.27cm^{3}$

$50.27cm^{3}$

$\dpi{100} 27.50cm^{3}$

Correct answer:

$50.27cm^{3}$

Explanation:

In order to solve this problem, one key fact needs to be understood. A sphere will take up exactly $\frac{2}{3}$ of the volume of a cylinder in which it is circumscribed. Therefore, if we find the volume of the sphere we can then solve for the volume of the cylinder.

First, we need to find the volume of the sphere.

$\dpi{100} V=\frac{4}{3}\pi (2cm)^{3}$

$\dpi{100} \dpi{100} V_{sphere}=10\frac{2}{3}\pi cm^{3}$

This equals $\frac{2}{3}$ of the volume of the cylinder. Therefore,

$\dpi{100} V_{cylinder}=\frac{3}{2}(10\frac{2}{3}\pi cm^{3})$

$\rightarrow 50.27cm^{3}$

Report an Error

Example Question #1 : How To Find The Volume Of A Cylinder

Calculate the volume of a cylinder with a height of six, and a base with a radius of three.

Possible Answers:

$54\pi$

$18\pi$

Correct answer:

$54\pi$

Explanation:

The volume of a cylinder is give by the equation $\small V=\pi r^2h$ .

In this example, $\small h=6$ and $\small r=3$ .

$V=\pi(3)^2(6)$

$V=\pi(9)(6)=54\pi$

Report an Error

Example Question #7 : How To Find The Volume Of A Cylinder

What is the volume of a cylinder with a circular side with a radius of and a length of ?

Possible Answers:

$84\pi$

$588\pi$

$334\pi$

$168\pi$

Correct answer:

$588\pi$

Explanation:

To find the volume of a cylinder we must know the equation for the volume of a cylinder which is

In this example the length is and the radius is so our equation will look like this $V=(12)(\pi)(7^{2})$

We then square the to get $7^{2}=49$

Then perform multiplication to get $(49)(12)(\pi)=588\pi$

The answer is $588\pi$ .

Report an Error

Example Question #11 : Cylinders

The volume of a cylinder is $54\pi$ units cubed. If the cylinder's height is units, what is its radius?

Possible Answers:

units

Correct answer:

units

Explanation:

The formula for the volume of a cylinder is $V = \pi r^2 \times h$ , where is volume, is the radius of the cylinder, and is its height. Substituing the given information into this equation makes it possible to find the radius by solving for :

$V = \pi r^2 \times h$

$\rightarrow 54\pi = \pi r^2 \times 6$

$\rightarrow \frac{54\pi}{6\pi} = \frac{(\pi r^2 \times 6)}{6\pi}$

$\rightarrow 9 = r^2$

$\rightarrow r = 3$ units

Report an Error

Example Question #651 : Geometry

This figure is a right cylinder with radius of 2 m and a height of 10 m.

What is the volume of the right cylinder (m³)?

Possible Answers:

125.66

150.80

125.71

62.83

25.13

Correct answer:

125.71

Explanation:

The formula for the volume of a right cylinder is $\pi r^{2}h$ where is the radius and is the height. Thus for this problem

$\pi\cdot2^{2}\cdot10=125.71$

Report an Error

Example Question #21 : Cylinders

What is the volume of a cylinder with a radius of and a height of ?

Possible Answers:

$9\pi$

$9\pi+15$

$54\pi$

$135\pi$

$96\pi$

Correct answer:

$135\pi$

Explanation:

When thinking of a 3D figure, think of it as a stack of something. In this case, a cylinder is a stack of a circles.

The volume will be the area of that base circle times the height of the cylinder. Mathematically that would be $V=(\pi r^2)*h$ .

Plug in our given values and solve.

$V=(\pi r^2)*h$

$V=(\pi (3)^2)*15$

$V=9\pi*15$

$V=135\pi$

Report an Error

Example Question #117 : Solid Geometry

Find the volume of a cylinder given that its height and radius are 4 and 11, respectively.

Possible Answers:

$312\pi$

$484\pi$

$225\pi$

$144\pi$

$121\pi$

Correct answer:

$484\pi$

Explanation:

The standard equation to find the volume of a cylinder is

$V=\pi hr^2$

where denotes height and denotes radius.

Plug in the given values for height and radius to find the volume of the cylinder:

$V=\pi \cdot 4(11)^2=4\cdot 121\cdot\pi =484\pi$

Report an Error

Example Question #118 : Solid Geometry

Find the volume of the following cylinder.

Cylinder

Possible Answers:

$545 \pi m^3$

$556 \pi m^3$

$539 \pi m^3$

$530 \pi m^3$

$521 \pi m^3$

Correct answer:

$539 \pi m^3$

Explanation:

The formula for the volume of a cylinder is:

$V = \pi r^2 h$

where is the radius of the base and is the length of the height.

Plugging in our values, we get:

$V = \pi (7m)^2 (11m)$

$V = 539 \pi m^3$

Report an Error

Example Question #1971 : High School Math

Find the volume of the following cylinder.

Cylinder

Possible Answers:

$144 \pi m^3$

$164 \pi m^3$

$154 \pi m^3$

$134 \pi m^3$

$124 \pi m^3$

Correct answer:

$144 \pi m^3$

Explanation:

The formula for the volume of a cylinder is:

V = (base)(height)

$V=(\pi r^2)(h)$

Where is the radius of the base and is the height of the cylinder

Plugging in our values, we get:

$V=\pi (4m)^2(9m)$

$V = 144 \pi m^3$

Report an Error

Example Question #22 : Cylinders

Find the volume of the following partial cylinder.

Cylinder_sector

Possible Answers:

$\frac{160 \pi m^3}{4}$

$\frac{160 \pi m^3}{2}$

$\frac{160 \pi m^3}{6}$

$160 \pi m^3$

$\frac{160 \pi m^3}{3}$

Correct answer:

$\frac{160 \pi m^3}{3}$

Explanation:

The formula for the volume of a partial cylinder is:

V = (base)(height)(part)

$V = (\pi r^2)(h)\left(\frac{part}{360}\right)$

Where is the radius of the cylinder, is the height of the cylinder, and part is the degrees of the sector.

Plugging in our values, we get:

$V = (\pi (8m)^2)(5m)\left(\frac{60}{360}\right)$

$V = \frac{320 \pi m^3}{6}=\frac{160 \pi m^3}{3}$

Report an Error

View Tutors

Melinda
Certified Tutor

Westminster College, Bachelor in Arts, Early Childhood Education.

View Tutors

Onyemaechi
Certified Tutor

Northwestern State University of Louisiana, Bachelor in Arts, Teaching English as a Second Language (ESL). University of Dall...

View Tutors

Loveleen
Certified Tutor

Maharishi Dayanand University, Master's/Graduate, Education.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in Seattle, SSAT Tutors in Boston, SSAT Tutors in Washington DC, ISEE Tutors in Miami, SAT Tutors in Dallas Fort Worth, MCAT Tutors in Chicago, English Tutors in New York City, LSAT Tutors in Phoenix, Math Tutors in San Francisco-Bay Area, Algebra Tutors in Chicago

Popular Courses & Classes

SSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Phoenix, Spanish Courses & Classes in Los Angeles, GMAT Courses & Classes in Miami, Spanish Courses & Classes in Chicago, ISEE Courses & Classes in New York City, ISEE Courses & Classes in Seattle, ISEE Courses & Classes in Houston, SSAT Courses & Classes in Atlanta, LSAT Courses & Classes in San Diego

Popular Test Prep

MCAT Test Prep in Denver, GRE Test Prep in Seattle, LSAT Test Prep in Washington DC, ISEE Test Prep in Washington DC, GRE Test Prep in Denver, GMAT Test Prep in Houston, LSAT Test Prep in Atlanta, LSAT Test Prep in Phoenix, SSAT Test Prep in Dallas Fort Worth, ISEE Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Solid Geometry

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #5 : How To Find The Volume Of A Cylinder

Example Question #1 : How To Find The Volume Of A Cylinder

Example Question #7 : How To Find The Volume Of A Cylinder

Example Question #11 : Cylinders

Example Question #651 : Geometry

Example Question #21 : Cylinders

Example Question #117 : Solid Geometry

Example Question #118 : Solid Geometry

Example Question #1971 : High School Math

Example Question #22 : Cylinders

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: