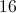All High School Math Resources
Example Questions
Example Question #2 : How To Find The Perimeter Of A Square
The diagonal of a square has a length of 10 inches. What is the perimeter of the square in inches squared?
Using the Pythagorean Theorem, we can find the edge of a side to be √50, by 2a2=102. This can be reduced to 5√2. This can then be multiplied by 4 to find the perimeter.
Example Question #231 : Plane Geometry
The area of square R is 12 times the area of square T. If the area of square R is 48, what is the length of one side of square T?
2
1
4
16
2
We start by dividing the area of square R (48) by 12, to come up with the area of square T, 4. Then take the square root of the area to get the length of one side, giving us 2.
Example Question #301 : Plane Geometry
When the side of a certain square is increased by 2 inches, the area of the resulting square is 64 sq. inches greater than the original square. What is the length of the side of the original square, in inches?
17
16
15
14
18
15
Let x represent the length of the original square in inches. Thus the area of the original square is x2. Two inches are added to x, which is represented by x+2. The area of the resulting square is (x+2)2. We are given that the new square is 64 sq. inches greater than the original. Therefore we can write the algebraic expression:
x2 + 64 = (x+2)2
FOIL the right side of the equation.
x2 + 64 = x2 + 4x + 4
Subtract x2 from both sides and then continue with the alegbra.
64 = 4x + 4
64 = 4(x + 1)
16 = x + 1
15 = x
Therefore, the length of the original square is 15 inches.
If you plug in the answer choices, you would need to add 2 inches to the value of the answer choice and then take the difference of two squares. The choice with 15 would be correct because 172 -152 = 64.
Example Question #1 : How To Find The Length Of The Side Of A Square
If the area of a square is 25 inches squared, what is the perimeter?
25
Not enough information
15
10
20
20
The area of a square is equal to length times width or length squared (since length and width are equal on a square). Therefore, the length of one side is 

Example Question #1 : How To Find The Length Of The Side Of A Square

A square is inscribed inside a circle, as illustrated above. The radius of the circle is 






Given that the square's diagonals pass through the circle's center, those diagonals must each form a diameter of the circle. The circle's diameter is twice its radius, i.e. 






Example Question #1 : How To Find If Quadrilaterals Are Similar
Quadrilateral ABCD contains four ninety-degree angles. Which of the following must be true?
I. Quadrilateral ABCD is a rectangle.
II. Quadrilateral ABCD is a rhombus.
III. Quadrilateral ABCD is a square.
I, II, and III
I and II only
II and III only
I only
II only
I only
Quadrilateral ABCD has four ninety-degree angles, which means that it has four right angles because every right angle measures ninety degrees. If a quadrilateral has four right angles, then it must be a rectangle by the definition of a rectangle. This means statement I is definitely true.
However, just because ABCD has four right angles doesn't mean that it is a rhombus. In order for a quadrilateral to be considered a rhombus, it must have four congruent sides. It's possible to have a rectangle whose sides are not all congruent. For example, if a rectangle has a width of 4 meters and a length of 8 meters, then not all of the sides of the rectangle would be congruent. In fact, in a rectangle, only opposite sides need be congruent. This means that ABCD is not necessarily a rhombus, and statement II does not have to be true.
A square is defined as a rhombus with four right angles. In a square, all of the sides must be congruent. In other words, a square is both a rectangle and a rhombus. However, we already established that ABCD doesn't have to be a rhombus. This means that ABCD need not be a square, because, as we said previously, not all of its sides must be congruent. Therefore, statement III isn't necessarily true either.
The only statement that has to be true is statement I.
The answer is I only.
Example Question #261 : Geometry
A quadrilateral with congruent sides is a __________.
square, rectangle, or rhombus
parallelogram
rectangle
square or rhombus
square or rhombus
A rhombus is any quadrilateral with four congruent sides. A square is a quadrilateral with four congruent sides and four right angles. A square is also a rhombus.
Rectangles will have two pairs of congruent sides, but not all four sides will be congruent.
Example Question #1 : Rhombuses
A quadrilateral ABCD has diagonals that are perpendicular bisectors of one another. Which of the following classifications must apply to quadrilateral ABCD?
I. parallelogram
II. rhombus
III. square
I and II only
I, II, and III
II and III only
I and III only
I and II only
If the diagonals of a quadrilateral are perpendicular bisectors of one another, then the quadrilateral must be a rhombus, but not necessarily a square. Since all rhombi are also parallelograms, quadrilateral ABCD must be both a rhombus and parallelogram.
Example Question #674 : High School Math
This figure is a rhombus with a side of 8 in.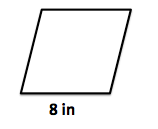
What is the area of the rhombus (in2)?
Not enough information
Not enough information
In order to determine the area of a rhombus you either need a base and a height OR the length of the two diagonals OR the base and an angle. Because we are only given the base with no information about the height, there is not enough information to determine the area of the rhombus.
Example Question #3 : Rhombuses
Find the area of the following rhombus:

The perimeter of the rhombus is 
The formula for the perimeter of a rhombus is:
Where 
Plugging in our values, we get:
The formula for the area of a rhombus is:
Where 

By drawing the diagonals, we create a right triangle with the hypotenuse as 

Since we know that 

Plugging in our values, we get:
Certified Tutor
All High School Math Resources