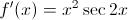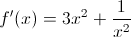All High School Math Resources
Example Questions
Example Question #62 : Derivatives
An ellipse is represented by the following equation:
What is the slope of the curve at the point (3,2)?
undefined
It would be difficult to differentiate this equation by isolating 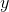



(Remember, 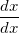


Now we need to isolate 
This is the equation for the derivative at any point on the curve. By substituting in (3, 2) from the original question, we can find the slope at that particular point:
Example Question #1 : Specific Derivatives
Find the derivative 
The derivative must be computed using the product rule. Because the derivative of 


Example Question #61 : Derivatives
Give the instantaneous rate of change of the function 

The instantaneous rate of change of 






Example Question #1223 : Ap Calculus Ab
What is 
Therefore,



Example Question #3 : Specific Derivatives
What is 
Therefore,



Example Question #1231 : Ap Calculus Ab
Find the derivative of the following function:
The derivative of 

Our function
the factor of 3 does not change when we differentiate, therefore the answer is
Example Question #1232 : Ap Calculus Ab
The derivative of a sine function does not follow the power rule. It is one that should be memorized.

Example Question #1 : Understanding Derivatives Of Trigonometric Functions
What is the second derivative of 
The derivatives of trig functions must be memorized. The first derivative is:

To find the second derivative, we take the derivative of our result.

Therefore, the second derivative will be 
Example Question #2 : Understanding Derivatives Of Trigonometric Functions
Compute the derivative of the function 
Use the Chain Rule.
Set 
Example Question #6 : Specific Derivatives
Find the derivative of the following function:
Since this function is a polynomial, we take the derivative of each term separately.
From the power rule, the derivative of
is simply
We can rewrite 
and using the power rule again, we get a derivative of

So the answer is
Certified Tutor
Certified Tutor
All High School Math Resources





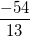





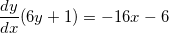













![f'(x) =\frac{\mathrm{d}}{\mathrm{d} x}\left [ \left ( \frac{1}{3} \right ) ^{x }\right ] = \ln \frac{1}{3} \cdot \left ( \frac{1}{3} \right) ^{x }= -\frac{ \ln 3}{3^{x}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/121386/gif.latex)