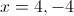We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Solving and Graphing Exponential Equations

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #115 : Algebra Ii

Find the vertical asymptote(s) of $y=\frac{x^3+2x+8}{x^2-36}$ .

Possible Answers:

x=-6 and x=6

x=36

x=6

There are no real vertical asymptotes.

$x=\frac{3}{2}$

Correct answer:

x=-6 and x=6

Explanation:

To find the vertical asymptotes, we set the denominator of the fraction equal to zero, as dividing anything by zero is "undefined." Since it's undefined, there's no way for us to graph that point!

Take our given equation, $y=\frac{x^3+2x+8}{x^2-36}$ , and now set the denominator equal to zero:

0=x^2-36 .

36=x^2

$\sqrt{36}=\sqrt{x^2}$

Don't forget, the root of a positive number can be both positive or negative ( -6^2=36 as does 6^2 ), so our answer will be $\pm6=x$ .

Therefore the vertical asymptotes are at x=-6 and x=6 .

Report an Error

Example Question #21 : Exponents

Find the horizontal asymptote(s) of $y=\frac{x^3+2x+8}{x^2-36}$ .

Possible Answers:

There are no real horizontal asymptotes.

y=0

$y=\frac{3}{2}$

y=1

y=6 and y=-6

Correct answer:

There are no real horizontal asymptotes.

Explanation:

To find the horizontal asymptote of the function, look at the variable with the highest exponent. In the case of our equation, $y=\frac{x^3+2x+8}{x^2-36}$ , the highest exponent is x^3 in the numerator.

When the variable with the highest exponent is in the numberator, there are NO horizontal asymptotes. Horizontal asymptotes only appear when the greatest exponent is in the denominator OR when the exponents have same power in both the denominator and numerator.

Report an Error

Example Question #1 : Quadratic Functions

What are the -intercepts of the equation?

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

x=4,-4

x=3

There are no -intercepts.

x=3,-3

x=2

Correct answer:

x=3,-3

Explanation:

To find the x-intercepts of the equation, we set the numerator equal to zero.

0=x^2-9

9=x^2

$\sqrt{9}=\sqrt{x^2}$

3,-3=x

Report an Error

Example Question #1 : Solving Exponential Functions

Find the vertical asymptote of the equation.

$y=\frac{x^2-9}{x^2-16}$

Possible Answers:

x=4, -4

x=4

There are no vertical asymptotes.

x=1

x=0

Correct answer:

x=4, -4

Explanation:

To find the vertical asymptotes, we set the denominator of the function equal to zero and solve.

0=x^2-16

16=x^2

$\sqrt{16}=\sqrt{x^2}$

4, -4=x

Report an Error

Example Question #11 : Understanding Asymptotes

$y=\frac{x^2-64}{x+2}$

What is the horizontal asymptote of this equation?

Possible Answers:

y=-2

y=1

There is no horizontal asymptote.

y=32

y=0

Correct answer:

There is no horizontal asymptote.

Explanation:

Since the exponent of the leading term in the numerator is greater than the exponent of the leading term in the denominator, there is no horizontal asymptote.

Report an Error

Example Question #1 : Solving Exponential Equations

Which value for satisfies the equation $4^x = \frac{192}{x}$ ?

Possible Answers:

$\frac{2}{3}$

$\frac{3}{2}$

Correct answer:

Explanation:

is the only choice from those given that satisfies the equation. Substition of for gives:

$4^3 = \frac{192}{3} \rightarrow 64 = 64$

Report an Error

Example Question #2 : Solving Exponential Equations

Solve for :

2x^2 - 32 =0

Possible Answers:

x = 16

x = -4

$x = \{-4, 0, 4\}$

$x = \{-4, 4\}$

x = 4

Correct answer:

$x = \{-4, 4\}$

Explanation:

To solve for in the equation 2x^2 - 32 =0

Factor out of the expression on the left of the equation:

$\rightarrow 2(x^2 - 16) =0$

Use the "difference of squares" technique to factor the parenthetical term on the left side of the equation.

$\rightarrow 2(x+4)(x-4)=0$

Any variable that causes any one of the parenthetical terms to become will be a valid solution for the equation. x+4 becomes when is , and x-4 becomes when is , so the solutions are and .

Report an Error

Example Question #1 : Solving Exponential Equations

Solve for (nearest hundredth):

$8^{y} = 100$

Possible Answers:

1.23

2.21

2.53

1.10

1.78

Correct answer:

2.21

Explanation:

Take the common logarithm of both sides and solve for :

$8^{y} = 100$

$\log 8^{y} = \log 100$

$y \log 8 =2$

$y =\frac{2}{\log 8} \approx \frac{2}{0.9031} \approx 2.21$

Report an Error

Example Question #1 : Solving Exponential Equations

Solve for (nearest hundredth):

$4 ^{2x - 7} = \frac{1}{256}$

Possible Answers:

x=-4

x=2

x = - 5.5

x = 1.5 x = 1 .5

x = 5.5

Correct answer:

x = 1.5 x = 1 .5

Explanation:

$\frac{1}{256} = \frac{1}{4 ^{4}} = 4 ^{-4}$ , so $4 ^{2x - 7} = \frac{1}{256}$ can be rewritten as

$4 ^{2x - 7} = 4 ^{-4}$

$\log_{4} 4 ^{2x - 7} =\log_{4} 4 ^{-4}$

2x - 7 = -4

2x - 7 + 7 = -4+ 7

2x = 3

x = 1 .5

Report an Error

Example Question #5 : Solving Exponential Equations

Solve for (nearest hundredth):

$80 ^{t} = 39$

Possible Answers:

t=1.20

t=0.62

t=0.72

t=0.31

t =0.84

Correct answer:

t =0.84

Explanation:

One method: Take the natural logarithm of both sides and solve for :

$80 ^{t} = 39$

$\ln 80 ^{t} = \ln 39$

$t \ln 80 = \ln 39$

$t =\frac{ \ln 39}{ \ln 80} \approx \frac{ 3.66}{ 4.38} \approx 0.84$

Report an Error

View Tutors

Kaylee
Certified Tutor

Brigham Young University, Bachelor, MFA - Animation.

View Tutors

Angela
Certified Tutor

North Georgia College State University, Bachelor of Science, Special Education. North Georgia College State University, Mas...

View Tutors

Dereika
Certified Tutor

Southern University and A & M College, Bachelor of Science, Accounting. Grand Canyon University, Master of Science, Accounting.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Statistics Tutors in Boston, Computer Science Tutors in Denver, Algebra Tutors in Boston, MCAT Tutors in Los Angeles, Algebra Tutors in Dallas Fort Worth, ACT Tutors in Atlanta, LSAT Tutors in Dallas Fort Worth, GMAT Tutors in Phoenix, Statistics Tutors in Phoenix, ISEE Tutors in Denver

Popular Courses & Classes

ACT Courses & Classes in Phoenix, Spanish Courses & Classes in Atlanta, SSAT Courses & Classes in New York City, SSAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Boston, LSAT Courses & Classes in Washington DC, GRE Courses & Classes in Philadelphia, LSAT Courses & Classes in San Francisco-Bay Area, SAT Courses & Classes in Seattle, ISEE Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Denver, ACT Test Prep in Phoenix, LSAT Test Prep in New York City, SAT Test Prep in Houston, SAT Test Prep in Philadelphia, LSAT Test Prep in Miami, SSAT Test Prep in Phoenix, LSAT Test Prep in San Diego, MCAT Test Prep in New York City, LSAT Test Prep in Los Angeles

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Solving and Graphing Exponential Equations

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #115 : Algebra Ii

Example Question #21 : Exponents

Example Question #1 : Quadratic Functions

Example Question #1 : Solving Exponential Functions

Example Question #11 : Understanding Asymptotes

Example Question #1 : Solving Exponential Equations

Example Question #2 : Solving Exponential Equations

Example Question #1 : Solving Exponential Equations

Example Question #1 : Solving Exponential Equations

Example Question #5 : Solving Exponential Equations

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: