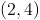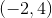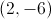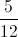All High School Math Resources
Example Questions
Example Question #11 : Midpoint And Distance Formulas
What is the midpoint of a line segment whose endpoints are 
The midpoint is the average of the endpoints.
Example Question #11 : Coordinate Geometry
What is the midpoint of a line segment connecting the points 

Use the midpoint formula, 


Example Question #12 : Coordinate Geometry
Find the midpoint between these two points:

To find the midpoint of a line segment, use the standard midpoint equation:
Plug in the given points and simplify:
Example Question #13 : Midpoint And Distance Formulas
Find the midpoint of the line segment connecting 

To find the midpoint of a line segment, we find the average of the 

Midpoint =
Example Question #1 : How To Find The Endpoints Of A Line Segment
What is the length of a line with endpoints 

The formula for the length of a line is very similiar to the pythagorean theorem:
Plug in our given numbers to solve:
Example Question #2 : How To Find The Endpoints Of A Line Segment
The points A, B, and C reside on a line segment. B is the midpoint of AC. If line AB measures 6 units in length, what is the length of line AC?
If B is the midpoint of AC, then AC is twice as long as AB. We are told that AB=6.
The diagram shows six units between points A and B, with B as the midpoint of segment AC. Therefore segment BC is also six units long, so line AC is twelve units long.
Example Question #13 : Coordinate Geometry
What is the length of a line segment with end points 

The formula for the length of line is the distance formula, which is very similar to the Pythagorean theorem.
Plug in the given values and solve for the length.
Example Question #14 : Coordinate Geometry
What would be the length of a line with endpoints at 

The formula for the length of line is the distance formula, which is very similar to the Pythagorean theorem.
Plug in the given values and solve for the length.
Example Question #1 : How To Find The Length Of A Line With Distance Formula
What line goes through the points 

Find the slope between the two points:
Next, use the slope-intercept form of the equation:


So the equation becomes 

Example Question #2 : How To Find The Length Of A Line With Distance Formula
What is the length of a line with endpoints at 

The formula for the length of a line is very similiar to the pythagorean theorem:
Plug in our given numbers to solve:
All High School Math Resources