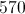High School Math : Algebra II
Study concepts, example questions & explanations for High School Math
All High School Math Resources
Example Questions
Example Question #1 : How To Find Z Scores For A Data Set
A population of values has a mean of 43 and a standard deviation of 12. One of the values in the population is 49. What is the Z-score for that value?
A Z-score indicates whether a particular value is typical for a population or data set. The closer the Z-score is to 0, the closer the value is to the mean of the population and the more typical it is. The Z-score is calculated by subtracting the mean of a population from the particular value in question, then dividing the result by the population's standard deviation.
Example Question #1 : Identifying Variables And Relationships
In a standard deck of cards, with replacement, what is the probability of drawing two Ace of Hearts?
Probability of drawing first ace of hearts:
Probability of drawing second ace of hearts:
Multiply both probabilities by each other:
Example Question #2 : How To Use The Multiplication Rule
In a standard deck of cards, without replacement, what is the probability of drawing three kings?
Start with 52 cards, probability of drawing first king:
Now you have 51 cards. Probability of drawing second king:
Now you have 50 cards. Probability of drawing third king:
Multiply all probabilities:
Example Question #403 : Algebra Ii
With a standard deck of cards, what is the probability of picking a spade then a red card if there is no replacement?
In a standard deck of cards:
Example Question #61 : Ap Statistics
Using a standard deck of cards, what is the probability of choosing a single face card?
There are 
Thus the probability of choosing a single face card is 
Example Question #401 : Algebra Ii
The horizontal line in the box of the box and whisker plot represents _____________.
Mean
Mode
Median
Range
Interquartile range
Median
A box and whisker plot separates the data into quartiles so that each quartile has an equal number of data points. The box indicates the interquartile range, that is, the top line of the box is the third quartile and the bottom line of the box is the second quartile. The line separating the second and third quartiles indicates the median. The lines outside of the box indicate the outer-quartiles (first and fourth).
Example Question #2 : Graphing Data
Based on the scatter plot below, is there a correlation between the 
No; there is no correlation
Yes; negative exponential relationship
Yes; negative linear relationship
Yes; positive linear relationship
Yes; negative linear relationship
The data points follow an overall linear trend, as opposed to being randomly distributed. Though there are a few outliers, there is a general relationship between the two variables.
A line could accurately predict the trend of the data points, suggesting there is a linear correlation. Since the y-values decrease as the x-values increase, the correlation must be negative. We can see that a line connecting the upper-most and lower-most points would have a negative slope.
An exponential relationship would be curved, rather than straight.
Example Question #1 : How To Find The Range For A Set Of Data
Six homes are for sale and have the following dollar values in thousands of dollars:
535
155
305
720
315
214
What is the range of the values of the six homes?
The range is the simplest measurement of the difference between values in a data set. To find the range, one simply subtracts the lowest value from the greatest value, ignoring the others. Here, the lowest value is 155 and the greatest is 720.
Example Question #1 : How To Find The Range For A Set Of Data
Alice recorded the outside temperature at noon each day for one week. These were the results.
Monday: 78
Tuesday: 85
Wednesday: 82
Thursday: 84
Friday: 82
Saturday: 79
Sunday: 80
What is the range of temperatures?
The range is the simplest measurement of the difference between values in a data set. To find the range, simply subtract the lowest value from the greatest value, ignoring the others.
Example Question #11 : Basic Statistics
You are given the following data:
What is the range?
Recall that we find the range of a set of data by subtracting the smallest value from the largest value. In this case, the smallest value is 
All High School Math Resources
