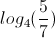We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Simplifying Logarithms

Simplify $log_{5}75 - log_{5}3$ .

Possible Answers:

0.75

1.50

Correct answer:

Explanation:

Using properties of logs we get:

$log_{5}75 - log_{5}3 = log_{5}\frac{75}{3}= log_{5}25$

$log_{5}25= log_{5}5^{2}= 2log_{5}5= 2\cdot 1=2$

Report an Error

Example Question #1 : Simplifying Logarithms

Simplify the following expression:

log(4) + log(12)

Possible Answers:

log(16)

log(48)

log(8)

log(3)

Correct answer:

log(48)

Explanation:

Recall the log rule:

log(a) + log(b) = log(ab)

In this particular case, a = 4 and b = 12 . Thus, our answer is $log(4\cdot 12) = log(48)$ .

Report an Error

Example Question #1 : Simplifying Logarithms

Use the properties of logarithms to solve the following equation:

$log_{6}(n-3)+log_{6}(n+2)=log_{3}(3)$

Possible Answers:

n=-3

n=4

n=3

n=-4

No real solutions

Correct answer:

n=4

Explanation:

Since the bases of the logs are the same and the logarithms are added, the arguments can be multiplied together. We then simplify the right side of the equation:

$log_{6}(n-3)+log_{6}(n+2)=log_{3}(3)$

$log_{6}(n-3)(n+2)=1$

The logarithm can be converted to exponential form:

$(n-3)(n+2)=6^{1}$

n^2-n-6=6

n^2-n-12=0

Factor the equation:

(n-4)(n+3)=0

n=4

Although there are two solutions to the equation, logarithms cannot be negative. Therefore, the only real solution is .

Report an Error

Example Question #1 : Simplifying Logarithms

Which of the following represents a simplified form of log(5x) ?

Possible Answers:

log(5)^x

5 * log(x)

log(5) + log(x)

log(5) * log(x)

$\frac{log(5) }{ log(x) }$

Correct answer:

log(5) + log(x)

Explanation:

The rule for the addition of logarithms is as follows:

log(ab) = log(a)+log(b) .

As an application of this, log(5x) = log(5)+log(x) .

Report an Error

Example Question #1 : Logarithms

Simplify the expression using logarithmic identities.

log_47-log_45

Possible Answers:

log_4(35)

$log_4(\frac{7}{5})$

$log_4(\frac{5}{7})$

log_4(2)

The expression cannot be simplified

Correct answer:

$log_4(\frac{7}{5})$

Explanation:

The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.

$log_A(\frac{B}{C})=log_AB-log_AC$

If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.

$log_AB-log_AC=log_A(\frac{B}{C})$

$A=4,\ B=7,\ C=5$

$log_47-log_45=log_4(\frac{7}{5})$

Report an Error

Example Question #2 : Logarithms

Evaluate by hand $\log_2(4^{\log_2(4^{5})})$

Possible Answers:

Cannot be found by hand

Correct answer:

Explanation:

Using the logarithm rules, exponents within logarithms can be removed and simply multiplied by the remaining logarithm. This expression can be simplified as $5\log_2(4)\log_2(4)$

Report an Error

Example Question #1 : Simplifying Logarithms

Solve for

log 2^x = 6

Possible Answers:

19.93

-8.6562

1.5897

Correct answer:

19.93

Explanation:

log 2^x = 6

Use the power reducing theorem:

$\log a^x = b \rightarrow x\log a = b$

a=2 and b=6

$x\log 2 = 6$

$x= \frac{6}{\log 2}$

x=19.93

Report an Error

Example Question #11 : Logarithms

Which of the following expressions is equivalent to log(2)^3 ?

Possible Answers:

log(8)

log(2) + 3

log(6)

log(5)

3*log(2)

Correct answer:

3*log(2)

Explanation:

According to the rule for exponents of logarithms, log(a)^b = b*log(a) . As a direct application of this, log(2)^3 = 3*log(2) .

Report an Error

Example Question #11 : Logarithms

Simplify the expression below.

$log(2 \cdot 2 \cdot 2)$

Possible Answers:

4log(2)

3log(2)

8log(2)

log(6)

log(5)

Correct answer:

3log(2)

Explanation:

Based on the definition of exponents, $log(2 \cdot 2 \cdot 2) = log (2^{3})$ .

Then, we use the following rule of logarithms:

$log(m^{n}) = n\cdot log(m)$

Thus, $log(2^{3}) = 3log(2)$ .

Report an Error

Example Question #151 : Algebra Ii

Solve the equation.

$3^{3x-7}=81^{12-3x}$

Possible Answers:

x=33

$x=\frac{11}{3}$

x=11

$x=\frac{22}{3}$

x=9

Correct answer:

$x=\frac{11}{3}$

Explanation:

Change 81 to 3^4 so that both sides have the same base. Once you have the same base, apply log to both sides so that you can set the exponential expressions equal to each other ( 3x-7 = 48-12x ). Thus, $x=\frac{11}{3}$ .

Report an Error

View Tutors

Soumya
Certified Tutor

Jawaharlal Nehru Technological University, Bachelor of Technology, Computer Science. Marquette University, Master of Science,...

View Tutors

Bobby
Certified Tutor

University of Houston - Downtown, Bachelor of Science, Applied Mathematics.

View Tutors

Reza
Certified Tutor

University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SAT Tutors in New York City, MCAT Tutors in Los Angeles, ACT Tutors in Boston, Biology Tutors in New York City, Algebra Tutors in San Diego, ISEE Tutors in Denver, Chemistry Tutors in Denver, French Tutors in Seattle, SAT Tutors in Boston, Physics Tutors in New York City

Popular Courses & Classes

LSAT Courses & Classes in San Francisco-Bay Area, LSAT Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in Phoenix, LSAT Courses & Classes in Boston, ISEE Courses & Classes in San Francisco-Bay Area, SSAT Courses & Classes in Seattle, SSAT Courses & Classes in Los Angeles, ACT Courses & Classes in Philadelphia, GMAT Courses & Classes in Denver, Spanish Courses & Classes in Los Angeles

Popular Test Prep

LSAT Test Prep in Chicago, SAT Test Prep in Los Angeles, GRE Test Prep in Phoenix, GMAT Test Prep in Denver, ISEE Test Prep in Denver, SSAT Test Prep in Washington DC, LSAT Test Prep in Dallas Fort Worth, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Philadelphia, MCAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Algebra II

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #1 : Logarithms

Example Question #2 : Logarithms

Example Question #1 : Simplifying Logarithms

Example Question #11 : Logarithms

Example Question #11 : Logarithms

Example Question #151 : Algebra Ii

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: