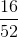Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Number Theory

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Understanding Real Numbers

Without using a calculator, which of the following is the best estimate for $\sqrt{90}$ ?

Possible Answers:

9.5

8.7

9.1

10.2

Correct answer:

9.5

Explanation:

We know that 9^2=81 and 10^2=100 .

81<90<100

$\sqrt{81}<\sqrt{90}<\sqrt{100}$

$9<\sqrt{90}<10$

Because 90 falls is approximately halfway between 81 and 100, the square root of 90 is approximately halfway between 9 and 10, or 9.5.

Report an Error

Example Question #2 : Understanding Real Numbers

Place in order from smallest to largest:

$\frac{3}{4},\; \; \frac{1}{8},\; \; \frac{5}{8},\; \; \frac{1}{6},\; \; \frac{1}{2},\; \; \frac{1}{5},\; \; \frac{1}{3}$

Possible Answers:

$\frac{1}{2},\; \; \frac{3}{4},\; \; \frac{1}{6},\; \; \frac{5}{8},\; \; \frac{1}{3},\; \; \frac{1}{5},\; \; \frac{1}{8}$

$\frac{1}{8},\; \; \frac{1}{6},\; \; \frac{1}{5},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{3}{4}$

$\frac{1}{5},\; \; \frac{3}{4},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{1}{8},\; \; \frac{1}{6}$

$\frac{1}{2},\; \; \frac{1}{3},\; \; \frac{3}{4},\; \; \frac{1}{5},\; \; \frac{1}{6},\; \; \frac{1}{8},\; \; \frac{5}{8}$

$\frac{1}{8},\; \; \frac{1}{5},\; \; \frac{1}{2},\; \; \frac{3}{4},\; \; \frac{1}{6},\; \; \frac{1}{3},\; \; \frac{5}{8}$

Correct answer:

$\frac{1}{8},\; \; \frac{1}{6},\; \; \frac{1}{5},\; \; \frac{1}{3},\; \; \frac{1}{2},\; \; \frac{5}{8},\; \; \frac{3}{4}$

Explanation:

To place in order, first we must find a common denominator and convert all fractions to that denominator.

$2, \;4,\; 8$ have a common denominator of .

$6,\; 3$ have a common denominator of .

6, 8, 5 have a common denominator of 120 .

Therefore we can use common denominators to make all of the fractions look similar. Then the ordering becomes trivial.

$\frac{1}{8}=\frac{15}{120},\; \; \frac{1}{6}=\frac{20}{120},\; \; \frac{1}{5}=\frac{24}{120}$

$\frac{1}{3}=\frac{40}{120},\; \; \frac{1}{2}=\frac{60}{120}$

$\frac{5}{8}=\frac{75}{120},\; \; \frac{3}{4}=\frac{90}{120}$

Report an Error

Example Question #3 : Understanding Real Numbers

What number is $20\%$ of ?

Possible Answers:

Correct answer:

Explanation:

For percent problems there are verbal cues:

"IS" means equals and "OF" means multiplication.

Then the equation to solve becomes:

$n=0.20\cdot 15=3$

Report an Error

Example Question #1 : Number Theory

Which of the following is NOT a real number?

Possible Answers:

$\sqrt{-9}$

$4i^{2}$

$\sqrt{84}$

$4\pi$

Correct answer:

$\sqrt{-9}$

Explanation:

We are looking for a number that is not real.

$4\pi$ , , and $\sqrt{84}$ are irrational numbers, but they are still real.

Then, $4i^{2}$ is equivalent to by the rules of complex numbers. Thus, it is also real.

That leaves us with: $\sqrt{-9}$ which in fact is imaginary (since no real number multiplied by itself yields a negative number) and simplifies to .

Report an Error

Example Question #1 : Understanding Real Numbers

Which of the following are considered real numbers?

Possible Answers:

$\pi$

1.9344

$\textup{All of the above}$

$\frac{3}{2}$

Correct answer:

$\textup{All of the above}$

Explanation:

Real numbers can be found anywhere on a continuous number line ranging from negative infinity to positive infinity; therefore, all of the numbers are real numbers.

Report an Error

Example Question #1 : Number Theory

If a card is drawn randomly from a regular shuffled 52 card deck, what is the probability that the card is either a spade or a 3?

Possible Answers:

$\frac{4}{13}$

$\frac{7}{52}$

$\frac{17}{52}$

$\frac{5}{52}$

$\frac{2}{13}$

Correct answer:

$\frac{4}{13}$

Explanation:

How many cards in the deck are either a spade or a 3?

There are thirteen spades, including a 3 of spades.

There are four 3's, including a 3 of spades.

Since we are counting the same card (3 of spades) twice, there are actually

13+4-1

=16 distinct cards that fit the criteria of being either a spade or a 3.

Since any of the 52 cards is equally likely to be drawn, the probability that it is a spade or a 3, is

$\frac{16}{52}$ $=\frac{4}{13}$

Report an Error

Example Question #2 : Number Theory

Find the distance between and on a number line.

Possible Answers:

7.5

10.25

Correct answer:

Explanation:

To find the distance on a number line:

$d=x_{2}-x{{_1}}$

d=11-(-4)

d=11+4

d=15

Report an Error

View Tutors

Donald
Certified Tutor

Queen's University, Bachelor in Arts, Mathematics.

View Tutors

Kaye
Certified Tutor

Loyola University-Chicago, Bachelor in Arts, English. Loyola University-Chicago, Masters in Education, Reading Teacher Educat...

View Tutors

Andrea
Certified Tutor

St Josephs University, Bachelor of Education, Elementary School Teaching. St Josephs University, Masters in Education, Readin...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Seattle, Computer Science Tutors in Los Angeles, ACT Tutors in Chicago, ISEE Tutors in Chicago, GMAT Tutors in Los Angeles, Reading Tutors in Denver, SSAT Tutors in Boston, ISEE Tutors in San Diego, SSAT Tutors in Los Angeles, MCAT Tutors in New York City

Popular Courses & Classes

MCAT Courses & Classes in Atlanta, SSAT Courses & Classes in Boston, ISEE Courses & Classes in Atlanta, SSAT Courses & Classes in Houston, SSAT Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Washington DC, MCAT Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Los Angeles, ISEE Courses & Classes in Chicago, Spanish Courses & Classes in Houston

Popular Test Prep

ACT Test Prep in Chicago, SSAT Test Prep in Chicago, GMAT Test Prep in Houston, ACT Test Prep in Los Angeles, MCAT Test Prep in Philadelphia, MCAT Test Prep in New York City, ISEE Test Prep in Atlanta, GMAT Test Prep in Chicago, MCAT Test Prep in Atlanta, SSAT Test Prep in Denver

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Number Theory

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #1 : Understanding Real Numbers

Example Question #2 : Understanding Real Numbers

Example Question #3 : Understanding Real Numbers

Example Question #1 : Number Theory

Example Question #1 : Understanding Real Numbers

Example Question #1 : Number Theory

Example Question #2 : Number Theory

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: