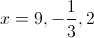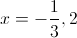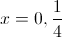We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 Next →

Example Question #4 : Solving Quadratic Equations

Find the zeros.

$f(x)=27x^{2}-45x-18$

Possible Answers:

$x=\frac{1}{3}$

$x=\frac{1}{3},2$

x=-2,-9

$x=9,-\frac{1}{3},2$

$x=-\frac{1}{3},2$

Correct answer:

$x=-\frac{1}{3},2$

Explanation:

Factor out a from the entire equation. After that, you get 9(3x^2-5x-2) . Factor the expression to (3x+1)(x-2) . Set both of those equal to zero and your answers are $-\frac{1}{3}$ and .

Report an Error

Example Question #5 : Solving Quadratic Equations

Find the zeros.

$f(x)=25x^{2}-81$

Possible Answers:

x=9,-9

$x=-\frac{9}{5}$

x=5

$x=\frac{9}{5}$

$x=\frac{9}{5},-\frac{9}{5}$

Correct answer:

$x=\frac{9}{5},-\frac{9}{5}$

Explanation:

This expression is the difference of perfect squares. Therefore, it factors to (5x-9)(5x+9) . Set both of those equal to zero and your answers are $\frac{9}{5}$ and $-\frac{9}{5}$ .

Report an Error

Example Question #6 : Solving Quadratic Equations

Find the zeros.

f(x)= 36x^2-9x

Possible Answers:

x=0,4

x=0

x=8

$x=\frac{1}{4}$

$x=0,\frac{1}{4}$

Correct answer:

$x=0,\frac{1}{4}$

Explanation:

Factor the equation to 9x(4x-1) . Set both equal to and you get and $\frac{1}{4}$ .

Report an Error

Example Question #1 : Solving Quadratic Equations

Find the zeros.

$f(x)=\frac{1}{4}x^2 +\frac{5}{4}x+\frac{3}{2}$

Possible Answers:

x=2

x=4,2

x=3,2

x=-3,3

x=-3,-2

Correct answer:

x=-3,-2

Explanation:

Factor a $\frac{1}{4}$ out of the quation to get

$\frac{1}{4}\left ( x^{2}+5x+6 \right )$

which can be further factored to

$\frac{1}{4}(x+3)(x+2)$ .

Set the last two expressions equal to zero and you get and .

Report an Error

Example Question #1 : Solving Quadratic Equations

Find the zeros.

f(x)=x(x-6)^2

Possible Answers:

x=0,6

x=0

x=6

x=1,-1

x=-6,6

Correct answer:

x=0,6

Explanation:

Set each expression equal to zero and you get 0 and 6.

Report an Error

Example Question #1 : Solving Quadratic Equations

Find the zeros.

f(x)=(x-2)(x+4)^3

Possible Answers:

x=-2,4

x=4

x=2,-4

x=2

x=0,2,-2

Correct answer:

x=2,-4

Explanation:

Set both expressions equal to . The first factor yields . The second factor gives you .

Report an Error

Example Question #1 : Solving Quadratic Equations

Find the zeros.

f(x)=(x+5)(x-8)^2

Possible Answers:

x=0

x=-8

x=-5,8

x=-5

x=5,8

Correct answer:

x=-5,8

Explanation:

Set both expressions to and you get and .

Report an Error

Example Question #61 : Intermediate Single Variable Algebra

Solve the following equation by factoring.

x^2+7x-8=0

Possible Answers:

$x=8\ or\ -1$

$x=-8\ or\ -1$

$x=8\ or\ 1$

$x=-8\ or\ 1$

Correct answer:

$x=-8\ or\ 1$

Explanation:

We can factor by determining the terms that will multiply to –8 and add to +7.

$8*-1=-8\ and\ 8+(-1)=7$

Our factors are +8 and –1.

0=x^2+7x-8=(x+8)(x-1)

Now we can set each factor equal to zero and solve for the root.

$x+8=0\ or\ x-1=0$

$x=-8\ or\ x=1$

Report an Error

Example Question #62 : Intermediate Single Variable Algebra

Solve the following equation by factoring.

2x^2-8x-10=0

Possible Answers:

$x=-5\ or\ -1$

$x=5\ or\ 1$

$x=-5\ or\ 1$

$x=5\ or\ -1$

Correct answer:

$x=5\ or\ -1$

Explanation:

We know that one term has a coefficient of 2 and that our factors must multiply to –10.

$2*-5=-10\ and\ 2+2(-5)=-8$

Our factors are +2 and –5.

0=2x^2-8x-10=(2x+2)(x-5)

Now we can set each factor equal to zero and solve for the root.

$2x+2=0\ or\ x-5=0$

$x=-1\ or\ 5$

Report an Error

Example Question #311 : Algebra Ii

Solve the following equation by factoring.

0=x^3+4x^2+4x

Possible Answers:

$x=0\ or\ -2$

$x= 0,2\ or\ -2$

$x=0,-4\ or\ 1$

$x=0\ or\ 2$

Correct answer:

$x=0\ or\ -2$

Explanation:

First, we can factor an term out of all of the values.

0=x^3+4x^2+4x=x(x^2+4x+4)

We can factor remaining polynomial by determining the terms that will multiply to +4 and add to +4.

$2*2=4\ and\ 2+2=4$

Our factors are +2 and +2.

0=x(x+2)(x+2)=x(x+2)^2

Now we can set each factor equal to zero and solve for the root.

$x=0\ or\ (x+2)^2=0$

$x=0\ or\ -2$

Report an Error

← Previous 1 2 3 4 5 6 7 8 9 10 11 12 Next →

View Tutors

Teagan
Certified Tutor

The University of Texas at Austin, Bachelor of Science, Physics.

View Tutors

Alan
Certified Tutor

Minnesota State University, Bachelor in Arts, Language Arts Teacher Education. College of St. Scholastica, Masters in Educati...

View Tutors

Ved
Certified Tutor

National Institute of Science Education and Research, Bachelor of Chemistry, Chemistry. University of Chicago, Doctor of Phil...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Spanish Tutors in Chicago, Math Tutors in Boston, Calculus Tutors in Los Angeles, LSAT Tutors in San Diego, SSAT Tutors in Atlanta, MCAT Tutors in Chicago, Computer Science Tutors in Philadelphia, Math Tutors in New York City, Statistics Tutors in Dallas Fort Worth, ACT Tutors in Philadelphia

Popular Courses & Classes

ACT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Francisco-Bay Area, ACT Courses & Classes in Dallas Fort Worth, GMAT Courses & Classes in San Diego, SAT Courses & Classes in Denver, LSAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Philadelphia, SSAT Courses & Classes in Washington DC, Spanish Courses & Classes in Los Angeles, MCAT Courses & Classes in Boston

Popular Test Prep

MCAT Test Prep in Seattle, ACT Test Prep in Houston, MCAT Test Prep in Phoenix, ACT Test Prep in Miami, SSAT Test Prep in San Diego, ACT Test Prep in Denver, SSAT Test Prep in New York City, GMAT Test Prep in San Diego, ISEE Test Prep in Miami, LSAT Test Prep in Seattle

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Intermediate Single-Variable Algebra

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #4 : Solving Quadratic Equations

Example Question #5 : Solving Quadratic Equations

Example Question #6 : Solving Quadratic Equations

Example Question #1 : Solving Quadratic Equations

Example Question #1 : Solving Quadratic Equations

Example Question #1 : Solving Quadratic Equations

Example Question #1 : Solving Quadratic Equations

Example Question #61 : Intermediate Single Variable Algebra

Example Question #62 : Intermediate Single Variable Algebra

Example Question #311 : Algebra Ii

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: