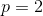All GRE Subject Test: Math Resources
Example Questions
Example Question #161 : Series In Calculus
For which values of p is

convergent?
Possible Answers:
only
All positive values of
it doesn't converge for any values of
Correct answer:
only
Explanation:
We can solve this problem quite simply with the integral test. We know that if
converges, then our series converges.
We can rewrite the integral as
and then use our formula for the antiderivative of power functions to get that the integral equals
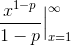
We know that this only goes to zero if 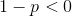

Reza
Certified Tutor
Certified Tutor
University of Sherbrooke, Doctor of Philosophy, Mathematics. University of Manitoba, Master of Science, Mathematics.
All GRE Subject Test: Math Resources
Popular Subjects
Computer Science Tutors in Chicago, SSAT Tutors in Dallas Fort Worth, LSAT Tutors in Philadelphia, English Tutors in New York City, GMAT Tutors in Philadelphia, LSAT Tutors in San Diego, SSAT Tutors in Los Angeles, ACT Tutors in New York City, Calculus Tutors in Los Angeles, Statistics Tutors in Atlanta
Popular Courses & Classes
Spanish Courses & Classes in Atlanta, Spanish Courses & Classes in San Diego, Spanish Courses & Classes in New York City, LSAT Courses & Classes in Houston, GMAT Courses & Classes in Atlanta, ACT Courses & Classes in New York City, ISEE Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Phoenix, SSAT Courses & Classes in San Diego, ACT Courses & Classes in Dallas Fort Worth
Popular Test Prep
ISEE Test Prep in Chicago, LSAT Test Prep in Chicago, ACT Test Prep in Dallas Fort Worth, ACT Test Prep in New York City, ISEE Test Prep in Denver, GRE Test Prep in Chicago, SAT Test Prep in Dallas Fort Worth, GMAT Test Prep in Atlanta, ISEE Test Prep in Seattle, ISEE Test Prep in Washington DC