All GRE Subject Test: Math Resources
Example Questions
Example Question #1 : Eigenvalues
Find the eigenvalues of the following matrix, if possible.
The eigenvalues do not exist.
In order to find the eigenvalues of a matrix, apply the following formula:

Compute the determinant and set it equal to zero.
Solve for lambda by using the quadratic formula.
Example Question #2 : Eigenspace Classifications
Find the eigenvalues of the following matrix, if possible.
The eigenvalues do not exist.
In order to find the eigenvalues of a matrix, apply the following formula:

Compute the determinant and set it equal to zero.
Solve for lambda by using the quadratic formula.
Example Question #1 : Abstract Algebra
Let 


What is the Lagrange error of the polynomial approximation to 
The fifth degree Taylor polynomial approximating 

The Lagrange error is the absolute value of the next term in the sequence, which is equal to .
We need only evaluate this at and thus we obtain
Example Question #2 : Abstract Algebra
Which of the following series does not converge?
We can show that the series 
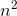

Alternatively, it's clear that 



The other series will converge by alternating series test, ratio test, geometric series, and comparison tests.
Example Question #2 : Groups
Find the minimum and maximum of 









There are no maximums or minimums


First we need to set up our system of equations.
Now lets plug in these constraints.
Now we solve for
If

If

Now lets plug in these values of 

We can conclude from this that 

Example Question #3 : Groups
Find the absolute minimum value of the function 

Let 

So this system of equations is



Taking partial derivatives and substituting as indicated, this becomes

From the left equation, we see either 






On the other hand, if instead 



Taking all four of our found points, and plugging them back into 

Hence the absolute minimum value is 
Certified Tutor
Certified Tutor
All GRE Subject Test: Math Resources






















![L = \lim_{n ->\infty } \frac{a_{n+1}}{a_{n}} = \lim_{n ->\infty } \left[\left(\frac{(n+1)!}{(n+1)^2 cos (n+1)} \div \frac{n!}{n^2 cos (n) }\right)\right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/343419/gif.latex)























