All GRE Subject Test: Chemistry Resources
Example Questions
Example Question #12 : Analytical Chemistry
Robert's work schedule for next week will be released today. Robert will work either 45, 40, 25, or 12 hours. The probabilities for each possibility are listed below:
45 hours: 0.3
40 hours: 0.2
25 hours: 0.4
12 hours: 0.1
What is the standard deviation of the possible outcomes?
There are four steps to finding the standard deviation of random variables. First, calculate the mean of the random variables. Second, for each value in the group (45, 40, 25, and 12), subtract the mean from each and multiply the result by the probability of that outcome occurring. Third, add the four results together. Fourth, find the square root of the result.
Example Question #13 : Analytical Chemistry
We have two independent, normally distributed random variables 








Normal distribution with mean 

Normal distribution with mean 

Normal distribution with mean 

Normal distribution with mean 

Normal distribution with mean 

The mean for any set of random variables is additive in the sense that
The difference is also additive, so we have
This means the mean of 

The variance is additive when the random variables are independent, which they are in this case. But it's additive in the sense that for any real numbers 

So for this difference, we have

So the mean and variance are 


Example Question #14 : Analytical Chemistry
A researcher performs a Bradford assay to determine the quantity of an unknown protein in his sample. The standard protein returns absorbance values of 0.101, 0.204, 0.302, 0.405 for the respective quantities of 10ug, 20ug, 30ug, and 40ug of protein. The unknown sample returns an absorbance value of 0.265. What is the quantity of protein in the unknown sample?
For this problem we need to determine the equation of our standard curve. This can be done by creating a graph from the data points and determining the slope.

Assuming that a sample of zero concentration will also have zero absorbance, we can find the equation for the line generated by finding the slope.
Pick two points on the line to find the slope. We will use (0,0) and (40,0.405).
Use this equation and the absorbance given in the question to find the concentration of the unknown sample.
Example Question #1 : Diagrams, Graphs, And Tables
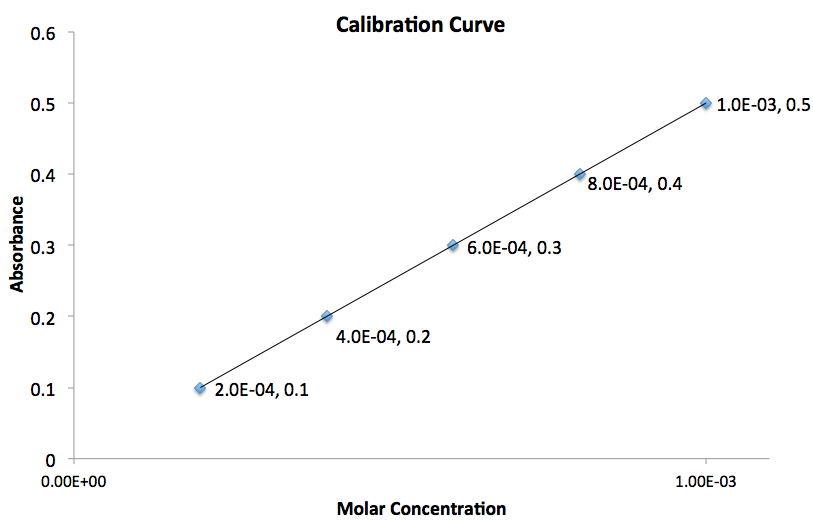
Using the graph given, what is the value for the slope of the line?
The slope of the line, 
The subscripts are simply the points you chose in the order you arbitrarily chose.The most important thing to do is plug the values into equation in the order you chose them.
To determine the slope of the line we need to use two points on the graph. Assuming the two points chosen correspond to 

Therefore the slope of the line is equal to
Example Question #15 : Analytical Chemistry
In the above reaction, by what factor would the reaction quotient change if the concentration of 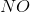
No change
For a general chemical equation 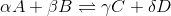
We can find the reaction quotient equation for our reaction by substituting the variables.
Notice that the concentration of 

Example Question #3 : Titration Curves
Consider the titration curve, in which an acid is treated with aqueous 0.5M NaOH.

The pH at the equivalence point was found to be 8.9. Approximately how many milliliters of 0.5M NaOH were needed to reach equivalence?
For any titration curve the equivalence point corresponds to the steepest part of the curve. In this case, the question indicates that the pH at equivalence was 8.9, which would correspond to a volume between 20.0 and 24.0 on the x-axis of the graph. This leads to our approximate answer of 21.8mL.
Example Question #4 : Titration Curves
Consider the titration curve, in which an acid is treated with aqueous 0.5M NaOH.

What is the approximate pKa of the starting acid?
The pKa corresponds to the pH when half of the acid has been neutralized. In this case, that would correspond to when half of the 0.5M NaOH has been added. We can see in the curve that the equivalence point is at around 22mL of NaOH, as this is the steepest change in pH. The half equivalence point will be found at approximately 11mL of NaOH addition. On the graph, 11mL of NaOH results in a pH of approximately 5.0, giving us our pKa value.
Example Question #1 : Acid Base Analysis

H2CO3 will have two equivalence points and two half equivalence points, one set corresponding to each of its two protons.
After the first equivalence point, all of the acid is in the form HCO3-. When an acid is at a half equivalence point, the acid's concentration will be equal to the concentration of the conjugate base. For the second half equivalence point, the acid is in the HCO3- form, and the conjugate base is CO32-. As a result, at the second half equivalence point, the concentrations of HCO3- and CO32- will be equal.
Example Question #2 : Acid Base Analysis
NaOH is added to a 500mL of 2M acetic acid. If the pKa value of acetic acid is approximately 4.8, what volume of 2M NaOH must be added so that the pH of the solution is 4.8?
250mL
2L
1L
500mL
250mL
To solve this question you need to think about the chemical reaction occurring.
We can ignore water and sodium ions for the sake of this question. The reactants exist in a 1:1 ratio, so that for every mol of NaOH we add, we lose one mol of acetic acid and gain one mol of acetate. We can determine the moles of acetic acid by using M = mol/L, which gives us mol = ML = (2M) * (0.5L) = 1mol acetic acid. If we use the Hendersen Hasselbach equation we can see that the pH equals the pKa when the concentration of conjugate base (acetate) equals the concentration of acid.
If we have 1mol of acetic acid and add 0.5mol of NaOH, we will lose 0.5mol of acetic acid and gain 0.5mol of acetate. We will then be at a point where acetic acid equals acetate. This is summarized in the ICE table below. Now we know the moles of NaOH (0.5 moles) and the concentration (2M) so we can find the volume by doing M = mol/L.
L = mol/M = (0.5mol)/(2M) = 0.25L
|
|
Acetic acid |
NaOH |
Acetate |
|
I |
1 mol |
0.5 mol |
0 mol |
|
C |
-0.5 mol |
-0.5 mol |
+0.5 mol |
|
E |
0.5 mol |
0 mol |
0.5 mol |
Example Question #1 : Henderson Hasselbalch Equation
The Ka for HCN is 
If there is a solution of 2M HCN, what concentration of NaCN is needed in order for the pH to be 9.2?
1M
No NaCN needs to be added
3M
2M
2M
To answer this question, we need to be able to compare the concentrations of acid and conjugate base in the solution with the pH. The Henderson-Hasselbach equation is used to compare these values, and is written as:![\small pH = pK_{a} + log\frac{[A^{-}]}{[HA]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86323/gif.latex)
Since we know the Ka of HCN, we can derive the pKa, which turns out to be 9.2.
As a result, we want to see to it that the amount of conjugate base is equal to the concentration of acid, so that ![\small log\frac{[A^{-}]}{[HA]} =0](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123433/gif.latex)
As a result, a concentration of 2M NaCN will allow the pH of the solution to be 9.2.
Certified Tutor
Certified Tutor
All GRE Subject Test: Chemistry Resources



























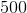



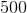
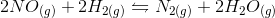




![Q=\frac{[C]^{\gamma}[D]^{\delta}}{[A]^{\alpha}[B]^{\beta}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668140/gif.latex)

![Q=\frac{[N_{2}][H_{2}O]^{2}}{[NO]^{2}{[H_{2}]}^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668141/gif.latex)
![Q_2=\frac{[N_{2}][H_{2}O]^{2}}{[2NO]^{2}{[H_{2}]}^{2}}=\frac{[N_{2}][H_{2}O]^{2}}{4[NO]^{2}{[H_{2}]}^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/668142/gif.latex)











![[CO_3^{2-}]=maximum\ value](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/183718/gif.latex)
![\small [HCO_{3}^{-}] = [CO_{3}^{2-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31451/gif.latex)
![\small [H_{2}CO_{3}] = [CO_{3}^{2-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31454/gif.latex)
![\small [H_{2}CO_{3}] = [HCO_{3}^{-}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31452/gif.latex)
![[HCO_3^-]=maximum\ value](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/31453/gif.latex)

![pH=pK_a+log\frac{[base]}{[acid]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/26258/gif.latex)
![9.2=-log(6.2*10^{-10})+log\frac{[CN^-]}{[HCN]}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123432/gif.latex)
![pH=9.2+log\frac{[CN^-]}{[HCN]}=9.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86324/gif.latex)
![pH=9.2+log\frac{[CN^-]}{[2]}=9.2](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86325/gif.latex)
![\frac{[CN^-]}{[2]}=1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/123434/gif.latex)
![[CN^-]=2M](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/86326/gif.latex)



