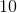All GRE Math Resources
Example Questions
Example Question #31 : Arithmetic Mean
If the average of 




70
80
150
40
90
80
If the average of 

Likewise, if the average of b and c is 110, then their sum must be 220.
Example Question #32 : How To Find Arithmetic Mean
The average of 10 test scores is 120 and the average of 30 additional scores is 100.
Quantity A: The weighted average of these scores
Quantity B: 105
Quantity B is greater
The relationship cannot be determined from the information given
The two quantities are equal
Quantity A is greater
The two quantities are equal
The sum of the first ten scores is 1,200 and the sum of the next 30 scores is 3,000. To take the weighted average of all scores, divide the sum of all scores (4,200) by the total number of scores (40), which would equal 105.
Example Question #31 : Arithmetic Mean
A plane flies from San Francisco to New York City at 600 miles per hour and returns along the same route at 400 miles per hour. What is the average flying speed for the entire route (in miles per hour)?
First, pick a distance, preferably one that is divisible by 400 and 600. As an example, we will use 1,200. If the distance is 1,200, then it took 2 hours to get to New York City and 3 hours to get back to San Francisco. So, the plane traveled 2,400 miles in 5 hours. The average speed is simply 2,400 miles divided by 5 hours, which is 480 miles per hour.
Example Question #32 : Arithmetic Mean
Column A: The median of the set
Column B: The mean of the set
Columns A and B are equal.
Column A is greater.
Column B is greater.
Cannot be determined.
Column B is greater.
The median is the middle number of the data set. If there is an even number of quantities in the data set, take the average of the middle two numbers.
Here, there are 8 numbers, so (18 + 20)/2 = 19.
The mean, or average, is the sum of the integers divided by number of integers in the set: (20 + 35 + 7 + 12 + 73 + 12 + 18 + 31) / 8 = 26
Example Question #47 : Arithmetic Mean
If the average (arithmetic mean) of 






There is not enough information to determine the answer.
If we can find the sum of 




Write out the average formula for the original three quantities. Remember, adding together and dividing by the number of quantities gives the average:
Isolate 
Write out the average formula for the new three quantities:
Combine the integers in the numerator:
Replace 
Example Question #571 : Gre Quantitative Reasoning
The arithmetic mean of a, b, and c is
Quantity A: The arithmetic mean of
Quantity B:
The two quantities are equal.
Quantity B is greater.
The relationship cannot be established.
Quantity A is greater.
The two quantities are equal.
To solve this problem, calculate Quantity A.
The arithmetic mean for a set of values is the sum of these values divided by the total number of values:
For the set 
Now recall that we're told that arithmetic mean of a, b, and c is 
Using this fact, return to what we've written for Quantity A:
Quantity B is also
So the two quantities are equal.
Example Question #34 : Arithmetic Mean
The arithmetic mean of a and b is
Quantity A:
Quantity B:
The two quantities are equal.
The relationship cannot be established.
Quantity B is greater.
Quantity A is greater.
Quantity A is greater.
The key to this problem is to recognize that Quantity A can be rewritten.
The function
can be written as
Now, recall what we're told about the mean of a and b, namely that it equals 
This is equivalent to saying
From this, we can see that
Therefore, we can find a value for Quantity A:
Quantity A is greater.
Example Question #33 : Arithmetic Mean
Looking at all the multiples of 5 from 5 to 50, what is the mean of all of those values?
All of the multiples of 5 from 5 to 50 are

The total of all of them is 275.
Then the mean will be 27.5

Example Question #38 : How To Find Arithmetic Mean
What is the average grade of a student who got a 









In order to solve this problem, we must know how to find the arithmetic mean for a set of numbers. The arithmetic mean is defined as the sum of all the numbers added up divided by the number. In this case, we first have to find the amount of credits present. Adding all the credits up, we find there are 15 credits. Now, by adding up the grades for each of those credits and dividing by the total number of credits, we can solve for the average grade of the student.
All GRE Math Resources