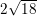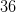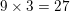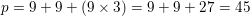GRE Math : Triangles
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #11 : How To Find The Perimeter Of An Acute / Obtuse Isosceles Triangle
The obtuse Isosceles triangle shown above has two sides with length 
To find the perimeter of this triangle, apply the perimeter formula:
Since, 
This triangle has two side lengths of 
Thus, the solution is:
Example Question #12 : Isosceles Triangles
A triangle has two sides with length 
The first step to solving this problem is that we must find the length of length 
Now, apply the formula:
Example Question #11 : Triangles
An isosceles triangle has an angle of 110°. Which of the following angles could also be in the triangle?
20
35
110
90
55
35
An isosceles triangle always has two equal angles. As there cannot be another 110° (the triangle cannot have over 180° total), the other two angles must equal eachother. 180° - 110° = 70°. 70° represents the other two angles, so it needs to be divided in 2 to get the answer of 35°.
Example Question #11 : Triangles
An isosceles triangle ABC is laid flat on its base. Given that <B, located in the lower left corner, is 84 degrees, what is the measurement of the top angle, <A?
Since the triangle is isosceles, and <A is located at the top of the triangle that is on its base, <B and <C are equivalent. Since <B is 84 degrees, <C is also. There are 180 degrees in a triangle so 180 - 84 - 84 = 12 degrees.
Example Question #12 : Triangles
Triangle ABC is isosceles
x and y are positive integers
A
---
x
B
---
y
Quantity B is greater
The relationship cannot be determined
The two quantities are equal
Quantity A is greater
Quantity B is greater
Since we are given expressions for the two congruent angles of the isosceles triangle, we can set the expressions equal to see how x relates to y. We get,
x – 3 = y – 7 --> y = x + 4
Logically, y must be the greater number if it takes x an additional 4 units to reach its value (knowing they are both positive integers).
Example Question #1 : How To Find An Angle In An Acute / Obtuse Isosceles Triangle
An isosceles triangle has one obtuse angle that is 
We know that an isosceles triangel has two equal sides and thus two equal angles opposite those equal sides. Because there is one obtuse angle of 112 degrees we automatically know that this angle is the vertex. If you sum any triangle's interior angles, you always get 180 degrees.
180 – 112 = 68 degrees. Thus there are 68 degrees left for the two equal angles. Each angle must therefore measure 34 degrees.
Example Question #1 : Acute / Obtuse Triangles
The obtuse Isosceles triangle shown above has two sides with length 
To solve this problem, apply the formula:
Side 
Since this is an Isosceles triangle, there must be two sides with a length of 
Thus, plug in each side lengths value to find the solution:
Example Question #11 : Triangles
The three angles in a triangle measure 3x, 4x + 10, and 8x + 20. What is x?
30
10
25
15
20
10
We know the angles in a triangle must add up to 180, so we can solve for x.
3x + 4x + 10 + 8x + 20 = 180
15x + 30 = 180
15x = 150
x = 10
Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle
In triangle ABC, AB=6, AC=3, and BC=4.
Quantity A Quantity B
angle C the sum of angle A and angle B
The relationship cannot be determined from the information given.
Quantity A is greater
Quantity A and B are equal
Quantity B is greater
Quantity A is greater
The given triangle is obtuse. Thus, angle 
Example Question #12 : Triangles
In the figure above, what is the value of angle x?
To find the top inner angle, recognize that a straight line contains 180o; thus we can subtract 180 – 115 = 65o. Since we are given the other interior angle of 30 degrees, we can add the two we know: 65 + 30 = 95o.
180 - 95 = 85
All GRE Math Resources
