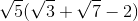To begin with, factor out the contents of the radicals.  This will make answering much easier:

$\displaystyle \sqrt{210}+\sqrt{55}=\sqrt{2*3*5*7}+\sqrt{5*11}$

They both have a common factor $\displaystyle 5$.  This means that you could rewrite your equation like this:

$\displaystyle \sqrt{5}\sqrt{2*3*7}+\sqrt{5}\sqrt{11}$

This is the same as:

$\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}$

These have a common $\displaystyle \sqrt{5}$.  Therefore, factor that out:

$\displaystyle \sqrt{5}\sqrt{42}+\sqrt{5}\sqrt{11}=\sqrt{5}(\sqrt{42}+\sqrt{11})$

These three roots all have a $\displaystyle 5$ in common; therefore, you can rewrite them:

$\displaystyle \sqrt{15}-\sqrt{20}+\sqrt{35}=\sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}$

Now, this could be rewritten:

$\displaystyle \sqrt{3*5}-\sqrt{4*5}+\sqrt{7*5}=\sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}$

Now, note that $\displaystyle \sqrt{4}=2$

Therefore, you can simplify again:

$\displaystyle \sqrt{5}\sqrt{3}-\sqrt{5}\sqrt{4}+\sqrt{5}\sqrt{7}=\sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}$

Now, that looks messy! Still, if you look carefully, you see that all of your factors have $\displaystyle \sqrt{5}$; therefore, factor that out:

$\displaystyle \sqrt{5}\sqrt{3}-2\sqrt{5}+\sqrt{5}\sqrt{7}=\sqrt{5}(\sqrt{3}-2+\sqrt{7})$

This is the same as:

$\displaystyle \sqrt{5}(\sqrt{3}+\sqrt{7}-2)$

Begin by factoring each of the roots to see what can be taken out of each:

$\displaystyle \sqrt{5^3}+\sqrt{7^2*5}+\sqrt{4^2*5}$

These can be rewritten as:

$\displaystyle 5\sqrt{5}+7\sqrt{5}+4\sqrt{5}$

Notice that each of these has a common factor of $\displaystyle \sqrt{5}$.  Thus, we know that we can rewrite it as:

$\displaystyle 5\sqrt{5}+7\sqrt{5}+4\sqrt{5} = \sqrt{5}(5+7+4) = 16\sqrt{5}$

Clearly, all three of these roots have a common factor $\displaystyle 10$ inside of their radicals. We can start here with our simplification. Therefore, rewrite the radicals like this:

$\displaystyle \sqrt{4}\sqrt{10}+\sqrt{2}\sqrt{10}+\sqrt{16}\sqrt{10}$

We can simplify this a bit further:

$\displaystyle 2\sqrt{10}+\sqrt{2}\sqrt{10}+4\sqrt{10} = 6\sqrt{10} + \sqrt{2}\sqrt{10}$

From this, we can factor out the common $\displaystyle \sqrt{10}$:

$\displaystyle 6\sqrt{10} + \sqrt{2}\sqrt{10} = \sqrt{10}(6+\sqrt{2})$

To attempt this problem, attempt to simplify the roots of the numerator and denominator:

$\displaystyle \frac{\sqrt{243}}{\sqrt{48}}=\frac{\sqrt{3*81}}{\sqrt{3*16}}$

Notice how both numerator and denominator have a perfect square:

$\displaystyle \frac{\sqrt{243}}{\sqrt{48}}=\frac{\sqrt{3*81}}{\sqrt{3*16}}=\frac{9\sqrt3}{4\sqrt3}$

The $\displaystyle \sqrt3$ term can be eliminated from the numerator and denominator, leaving

$\displaystyle \frac{9}{4}$

For this problem, begin by simplifying the roots. As it stands, numerator and denominator have a common factor of $\displaystyle 7$ in the radical:

$\displaystyle \frac{\sqrt{343}}{\sqrt{63}}=\frac{\sqrt{7*49}}{\sqrt{7*9}}$

And as it stands, this $\displaystyle 7$ is multiplied by a perfect square in the numerator and denominator:

$\displaystyle \frac{\sqrt{343}}{\sqrt{63}}=\frac{\sqrt{7*49}}{\sqrt{7*9}}=\frac{7\sqrt{7}}{3\sqrt{7}}$

The $\displaystyle \sqrt{7}$ term can be eliminated from the top and bottom, leaving

$\displaystyle \frac{7}{3}$

To solve this problem, try simplifying the roots by factoring terms; it may be noticeable from observation that both numerator and denominator have a factor of $\displaystyle 3$ in the radical:

$\displaystyle \frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}$

We can see that the denominator has a perfect square; now try factoring the $\displaystyle 50$ in the numerator:

$\displaystyle \frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}=\frac{\sqrt{3*2*25}}{4\sqrt{3}}$

We can see that there's a perfect square in the numerator:

$\displaystyle \frac{\sqrt{150}}{\sqrt{48}}=\frac{\sqrt{3*50}}{\sqrt{3*16}}=\frac{\sqrt{3*2*25}}{4\sqrt{3}}=\frac{5\sqrt{3*2}}{4\sqrt{3}}$

Since there is a $\displaystyle 3$ in the radical in both the numerator and denominator, we can eliminate it, leaving

$\displaystyle \frac{5\sqrt{2}}{4}$