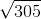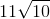All GRE Math Resources
Example Questions
Example Question #1 : Arithmetic
Neither x nor y is equal to 0.
xy = 4y/x
Quantity A: x
Quantity B: 2
Quantity A is greater.
The two quantities are equal.
Quantity B is greater.
The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Given xy = 4y/x and x and y not 0.
Therefore you are able to divide both sides by 'y' such that:
x = 4/x
Multiply both sides by x:
x2 = 4 or x = +2 or –2.
Because of the fact that x could equal –2, the relationship cannot be determined from the information given.
Example Question #1 : Basic Squaring / Square Roots
Quantity A:
Quantity B: 399
Quantity A is greater.
The two quantities are equal.
Quantitiy B is greater.
The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
Since 

Example Question #3 : Arithmetic
Quantity A: 9
Quantity B: √(25 + 55)
The relationship cannot be determined from the information given.
Quantity B is greater.
Quantity A is greater.
The two quantities are equal.
Quantity A is greater.
In order to determine the relationship between Quantity A and Quantity B, let's convert both to square roots. In order to do this, we must square Quantity A so it becomes √81 which is equivalent to 9. Now to Quantity B, we must simplify by adding the two values together (25 + 55) to get √80.
√81 is greater than the √80 because 81 is greater than 80. Thus Quantity A is greater.
Example Question #4 : Arithmetic
Simplify:
When simplifying the square root of a number that may not have a whole number root, it's helpful to approach the problem by finding common factors of the number inside the radicand. In this case, the number is 24,300.
What are the factors of 24,300?
24,300 can be factored into:
When there are factors that appear twice, they may be pulled out of the radicand. For instance, 100 is a multiple of 24,300. When 100 is further factored, it is 
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267786/gif.latex)
But 243 can also be factored:
Following the same principle as for the 100, the problem would become![9\cdot 10\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267789/gif.latex)
9 and 10 may be multiplied together, yielding the final simplified answer of
Example Question #1 : Arithmetic
To solve the equation 
When a factor appears twice, we can take it out of the square root.
Now the numbers can be added directly because the expressions under the square roots match.
Example Question #1 : Basic Squaring / Square Roots
Simplify.

To simplify, we must try to find factors which are perfect squares. In this case 16 is a factor of 624 and is also a perfect square.
Therefore we can rewrite the square root of 624 as:
Example Question #1 : Basic Squaring / Square Roots
Reduce 
To simplify, we must try to find factors which are perfect squares. In this case 20 is a factor of 400 and is also a perfect square.
Thus we can rewrite the problem as:
Note:
Example Question #1 : Arithmetic
Simplify.
Use the following steps to reduce this square root.
To simplify, we must try to find factors which are perfect squares. In this case 144 is a factor of 720 and is also a perfect square.
Thus we can rewrite the problem as follows.
Example Question #4 : Arithmetic
Find the square root of 
Use the following steps to find the square root of
To simplify, we must try to find factors which are perfect squares. In this case 900 is a factor of 1800 and is also a perfect square.
Thus we can rewrite the problem as follows.
Example Question #1 : Arithmetic
Simplify.
To simplify, we must try to find factors which are perfect squares. In this case 9 is a factor of 54 and is also a perfect square.
To reduce this expression, use the following steps:
All GRE Math Resources



![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267782/gif.latex)
![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267774/gif.latex)
![900\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267780/gif.latex)
![9\sqrt[2]{300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267781/gif.latex)
![90\sqrt[2]{270}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267776/gif.latex)
![10\sqrt[2]{243}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267778/gif.latex)
![\sqrt[2]{24,300}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267783/gif.latex)
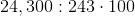


![90\sqrt[2]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/267790/gif.latex)