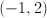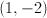GRE Math : How to find out if a point is on a line with an equation
Study concepts, example questions & explanations for GRE Math
All GRE Math Resources
Example Questions
Example Question #231 : Geometry
Find the point where the line y = .25(x – 20) + 12 crosses the x-axis.
(0,–28)
(12,0)
(–28,0)
(–7,0)
(0,0)
(–28,0)
When the line crosses the x-axis, the y-coordinate is 0. Substitute 0 into the equation for y and solve for x.
.25(x – 20) + 12 = 0
.25x – 5 = –12
.25x = –7
x = –28
The answer is the point (–28,0).
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
On a coordinate plane, two lines are represented by the equations 
You can solve for the 
Solve for 
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
If the two lines represented by 
Solve for 
Plugging 
These are the coordinates for the intersection of the two lines.
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
Determine the greater quantity:
or
The relationship cannot be determined.
The quantities are equal.
The quantities are equal.
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
Which of the following set of points is on the line formed by the equation 
The easy way to solve this question is to take each set of points and put it into the equation. When we do this, we find the only time the equation balances is when we use the points 
For practice, try graphing the line to see which of the points fall on it.
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
Consider the lines described by the following two equations:
4y = 3x2
3y = 4x2
Find the vertical distance between the two lines at the points where x = 6.
12
44
48
36
21
21
Since the vertical coordinates of each point are given by y, solve each equation for y and plug in 6 for x, as follows:
Taking the difference of the resulting y -values give the vertical distance between the points (6,27) and (6,48), which is 21.
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
For the line
Which one of these coordinates can be found on the line?
(3, 7)
(9, 5)
(6, –12)
(3, –6)
(6, 5)
(3, –6)
To test the coordinates, plug the x-coordinate into the line equation and solve for y.
y = 1/3x -7
Test (3,-6)
y = 1/3(3) – 7 = 1 – 7 = -6 YES!
Test (3,7)
y = 1/3(3) – 7 = 1 – 7 = -6 NO
Test (6,-12)
y = 1/3(6) – 7 = 2 – 7 = -5 NO
Test (6,5)
y = 1/3(6) – 7 = 2 – 7 = -5 NO
Test (9,5)
y = 1/3(9) – 7 = 3 – 7 = -4 NO
Example Question #91 : Lines
Solve the following system of equations:
–2x + 3y = 10
2x + 5y = 6
(–2, 2)
(3, –2)
(2, 2)
(3, 5)
(–2, –2)
(–2, 2)
Since we have –2x and +2x in the equations, it makes sense to add the equations together to give 8y = 16 yielding y = 2. Then we substitute y = 2 into one of the original equations to get x = –2. So the solution to the system of equations is (–2, 2)
Example Question #1 : How To Find Out If A Point Is On A Line With An Equation
Which of the following sets of coordinates are on the line 
Because this equation is true, the point must lie on the line. The other given answer choices do not result in true equalities.
Example Question #98 : Coordinate Geometry
Which of the following points can be found on the line 
We are looking for an ordered pair that makes the given equation true. To solve, plug in the various answer choices to find the true equality.
Because this equality is true, we can conclude that the point 
All GRE Math Resources
