All GRE Math Resources
Example Questions
Example Question #1 : How To Subtract Complex Fractions
Quantity A:
Quantity B:
The two quantities are equal.
The relationship between A and B cannot be determined.
Quantity B is greater.
Quantity A is greater.
Quantity A is greater.
As it is, quantities A and B have different denominators, so making a comparison can be tricky. Making a common denominator will allow for comparison of just the numerators, so that would make a good first step:
Quantity A:
Quantity B:
Disregarding equal denominators, since they'll always have a positive value, compare the numerators. If 


Quantity A is greater.
Example Question #2 : How To Subtract Complex Fractions
Quantity A:
Quantity B:
Quantity B is greater.
Quantity A is greater.
The relationship between A and B cannot be determined.
Quantity A and Quantity B are equal.
The relationship between A and B cannot be determined.
One way to approach this question is to try to reduce the complexity of each quantity. By subtracting the value of Quantity A, 
Quantity A':
Quantity B':
Now, it's easy to see that for different values of 
Since 
Example Question #3 : How To Subtract Complex Fractions
Rhoda can prune 





To find out how many rhododendrons Rita will need to prune in an hour, we must first find out how many she needs to prune.
If Rhoda can prune 







If this is not readily apparent, it can be found by finding out how many each prunes in one hour, then multiplying by 
Rhoda:
Rhonda:
Between Rhoda and Rhonda, 


Since she has 
Example Question #1 : Circles
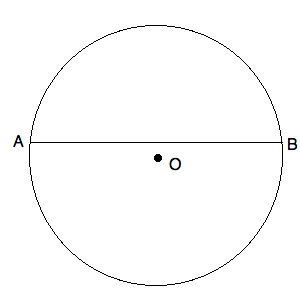
O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Which of the following is true?
Quantity B is greater.
Quantity A is greater.
The relationship cannot be determined.
The two quantities are equal.
Quantity A is greater.

O is the center of the circle above.
The length of 

Quantity A: The area of the circle.
Quantity B:
Do not be tricked by this question. It is true that 






Example Question #1 : Circles

O is the center of the circle above.
The circumference of the circle above is 
Quantity A: The length of 
Quantity B:
Which of the following is true?
Quantity B is larger.
Quantity A is larger.
The relationship cannot be determined.
The two quantities are equal.
Quantity B is larger.
Now, we know that the circumference of a circle is:

This means that the diameter of our circle is must be 


Example Question #1 : Circles
What is the circumference of a circle with an area of 36π?
None of the other answers
6π
32
12π
15π
12π
We know that the area of a circle can be expressed: a = πr2
If we know that the area is 36π, we can substitute this into said equation and get: 36π = πr2
Solving for r, we get: 36 = r2; (after taking the square root of both sides:) 6 = r
Now, we know that the circuference of a circle is expressed: c = πd. Since we know that d = 2r (two radii, placed one after the other, make a diameter), we can rewrite the circumference equation to be: c = 2πr
Since we have r, we can rewrite this to be: c = 2π*6 = 12π
Example Question #1 : Geometry
Which is greater: the circumference of a circle with an area of 

The perimeter of the square is greater.
The circumference of the circle is greater.
The relationship cannot be determined from the information given.
The two quantities are equal.
The circumference of the circle is greater.
Starting with the circle, we need to find the radius in order to get the circumference. Find 
Then calculate circumference:


To find the perimeter of the square, we can use 



Example Question #3 : Circles
Circle A has an area of 
Based on our information, we know that the 121π = πr2; 121 = r2; r = 11.
Our other circle with half the radius of A has a diameter equal to the radius of A. Therefore, the circumference of this circle is 11π. Half of this is 5.5π. However, since this is a semi circle, it is enclosed and looks like this:
Therefore, we have to include the diameter in the perimeter. Therefore, the total perimeter of the semi-circle is 5.5π + 11.
Example Question #2 : Geometry
Quantity A: The circumference of a circle with radius
Quantity B: The area of a circle with a diameter one fourth the radius of the circle in Quantity A
Which of the following is true?
The relationship between the two values cannot be determined.
Quantity A is larger.
Quantity B is larger.
The two quantities are equal.
The relationship between the two values cannot be determined.
Let's compute each value separately. We know that the radii are positive numbers that are greater than or equal to 

Quantity A
Since 
Quantity B
If the diameter is one-fourth the radius of A, we know:
Thus, the radius must be half of that, or 
Now, we need to compute the area of this circle. We know:
Therefore,
Now, notice that if 
However, if we choose a value like 
Quantity A:
Quantity B:
Therefore, the relation cannot be determined!
Example Question #7 : Circles

Circle 

The area of Square 


What is the circumference of Circle 






Since we know that the area of Square 











The circumference of this circle is defined as:

(You could also compute this from the diameter, but many students just memorize the formula above.)
All GRE Math Resources



















































