All GRE Math Resources
Example Questions
Example Question #2 : Ordering
8/9 > x > 6/7
Quantity A: x
Quantity B: 7/8
Quantity B is greater.
The two quantities are equal.
Quantity A is greater.
The relationship cannot be determined from the information given.
The relationship cannot be determined from the information given.
At first glance, it appears that both values are equal.7/8 and x will be between 6/7 and 8/9.
However do a quick calculation on the GRE calculator to figure out that 6/7 is approximately 0.857 and and 8/9 is approximately 0.889. 7/8 (Quantity B) is 0.875. x could equal 0.86 and be less than Quantity B or x could equal 0.88 and be greater than Quantity B. Because at least two possibilities exist (x could also equal 7/8), there is not enough information given to determine the relationship.
Example Question #584 : Arithmetic
Which of the following fractions is the greatest?
17/23
1/2
8/11
19/25
15/21
19/25
The trick here is to set 1/2 as a baseline; all other choices are greater than 1/2.
Next is to see how much the difference is between each numerator and denominator (if you multiply 8/11 by 2/2, it will become 16/22) - each fraction besides 1/2 has a numerator that is 6 units less than the denominator. The trick is that the largest numerator will be the largest fraction when the numerator and denominator are the same units apart on all fractions.
Example Question #3 : Ordering
Which is greater, 


The relationship cannot be determined from the information given.
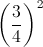
The quantities are equal.

To add fractions with the same denominator, add their numerators and leave the denominator the same:
To square a fraction, square its numerator and denominator:
For comparison, rewrite the first fraction with 16 as its denominator also:

Example Question #586 : Arithmetic
Quantitative Comparison
Quantity A:
Quantity B:
The relationship cannot be determined form the information given.
The two quantities are equal.
Quantity A is greater.
Quantity B is greater.
Quantity B is greater.
One option is to do the actual math to find the answer. Quantity A = 3/7 + 3/8 = 45/56. Quantity B = 13/14 + 4/5 = 121/70. Here Quantity A < 1 and Quantity B > 1, so it is easy to tell which is bigger. This isn't always the case however, so often doing the math is NOT the quickest or easiest way to solve GRE questions. For example, if the two answers had been 45/56 and 72/83, it would have been very difficult to tell which was the larger fraction just by looking at them.
Instead of computationally figuring this question out, we can break it into parts.
Let's look at the first fraction in the two columns: 3/7 < 1/2 and 13/14 > 1/2, so the first fraction in Quantity B is bigger.
Next look at the second fraction: 3/8 < 1/2 and 4/5 > 1/2, so the second fraction in Quantity B is bigger.
Now we know that Quantity B is bigger without having to do any real math!
Example Question #4 : Ordering
Which of these fractions is the LARGEST?
Now that the GRE has a built-in calculator, simply find the decimal equivalent of each of the answer choices to see which is the largest!
Example Question #591 : Arithmetic
Which of the following is the greatest fraction:
Since the fraction 
Example Question #1 : Complex Fractions
Solve:
To simplify a complex fraction, simply invert the denomenator and multiply by the numerator:
Multiplying the numerator by the reciprocal of the denominator for each term we get:
Since we have a common denominator we can now add these two terms.
Example Question #592 : Arithmetic
Simplify:
Although you could look for the common denominator of the fraction as it has been written, it is probably easiest to rewrite the fraction in slightly simpler terms. Thus, recall that you can rewrite your fraction as:
Using the rule for dividing fractions, you can rewrite your expression as:
Then, you can multiply each set of fractions, getting:
This makes things very easy, for then your value is:
Example Question #173 : Fractions
Simplify:
For this problem, begin by rewriting the complex fraction, using the rule for dividing fractions:
This is much easier to work on. Cancel out the 




The common denominator is 
Example Question #4 : How To Add Complex Fractions
Begin by simplifying all terms inside the parentheses. Begin with the innermost set. Find a common denominator for the two terms. In this case, the common denominator will be twenty:
Simplify 


Multiply the two fractions in the parentheses by multiplying straight across (A quick shortcut would be to factor out the 10 on top and bottom).
Now convert 

In order to subtract the two fractions, find a common denominator. In this case, it will be 70.
Now subtract, and find the answer!

All GRE Math Resources































































