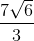Begin by factoring each of the roots to see what can be taken out of each:

These can be rewritten as:

Notice that each of these has a common factor of .  Thus, we know that we can rewrite it as:

Clearly, all three of these roots have a common factor  inside of their radicals. We can start here with our simplification. Therefore, rewrite the radicals like this:

We can simplify this a bit further:

From this, we can factor out the common :

To attempt this problem, attempt to simplify the roots of the numerator and denominator:

Notice how both numerator and denominator have a perfect square:

The  term can be eliminated from the numerator and denominator, leaving

For this problem, begin by simplifying the roots. As it stands, numerator and denominator have a common factor of  in the radical:

And as it stands, this  is multiplied by a perfect square in the numerator and denominator:

The  term can be eliminated from the top and bottom, leaving

To solve this problem, try simplifying the roots by factoring terms; it may be noticeable from observation that both numerator and denominator have a factor of  in the radical:

We can see that the denominator has a perfect square; now try factoring the  in the numerator:

We can see that there's a perfect square in the numerator:

Since there is a  in the radical in both the numerator and denominator, we can eliminate it, leaving

Take each fraction separately first:

(2√3)/(√2) = [(2√3)/(√2)] * [(√2)/(√2)] = (2 * √3 * √2)/(√2 * √2) = (2 * √6)/2 = √6

Similarly:

(4√2)/(√3) = [(4√2)/(√3)] * [(√3)/(√3)] = (4√6)/3 = (4/3)√6

Now, add them together:

√6 + (4/3)√6 = (3/3)√6 + (4/3)√6 = (7/3)√6

Begin by breaking down each of the roots in question.  Often, for the GRE, your answer arises out of doing such basic "simplification moves".

Quantity A

This is the same as:

, which can be reduced to:

Quantity B

This is the same as:

, which can be reduced to:

Thus, at the end of working through the proper math, you realize that the two values are equal!

Begin by factoring out each of the radicals:

For the first two radicals, you can factor out a  or :

The other root values cannot be simply broken down. Now, combine the factors with :

This is your simplest form.

Begin by getting your  terms onto the left side of the equation and your numeric values onto the right side of the equation:

Next, you can combine your radicals. You do this merely by subtracting their respective coefficients:

Now, square both sides:

Solve by dividing both sides by :

To solve this problem, we must realize that the only way to add or subtract square roots is if the number under to square root is equivalent to each other. Therefore we must find a way to simplify each square root.

First we attempt to simplify the first term,

We break apart the number under the square root and find

Simplifying

Therefore we know that in order to try and simplify the other terms, the number under the square root has to be 3. By removing  from the other terms in the equation, we will attempt to see if they can be simplified as well.

For the second term,

Finally for the last term,

Our new equation becomes 

Once all number under the square roots become the same, we can treat it as simple addition/subtraction and solve.