All GMAT Math Resources
Example Questions
Example Question #17 : Calculating Arithmetic Mean
Consider this data set:
Order the mean, median, mode, and midrange of the data set from least to greatest.
Median, mean, midrange, mode
Midrange, mean, median, mode
Midrange, median, mean, mode
Mean, median, midrange, mode
Median, midrange, mean, mode
Midrange, mean, median, mode
The mean of the data set is the sum of the elements divided by the size of the set, which is ten:
The median of a data set with an even number of elements is the arithmetic mean of the two elements that fall in the middle when the elements are arranged in ascending order. These two elements ar 6 and 7, so the median is 
The mode of the data set is the element which occurs the most frequently. Since 7 appears three times, 6 appears twice, and all other elements appear once, the mode is 7.
The midrange of the data set is the arithmetic mean of the least and greatest elements. These two elements are 1 and 10, so the midrange is 
The four quantities, in ascending order, are:
Midrange, mean, median, mode.
Example Question #31 : Descriptive Statistics
Consider the data set 
Which of the following is true about the median and the mean of the data set?
The mean and the median are equal.
The median exceeds the mean by 0.5.
The mean exceeds the median by 0.5.
The median exceeds the mean by 1.
The mean exceeds the median by 1.
The median exceeds the mean by 0.5.
The mean of the data set is the sum of the elements divided by the size of the set, which is ten:
The median of a data set with an even number of elements is the arithmetic mean of the two elements that fall in the middle when the elements are arranged in ascending order. These two elements are 6 and 7, so the median is 
The median is greater than the mean by 
Example Question #22 : Arithmetic Mean
The mean of the following terms is 11. Solve for 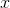
15, 12, 9, 7, 17, 8,
The mean times the number of terms is equal to 77.
The sum of all of the terms must equal 77.
Example Question #32 : Descriptive Statistics
Charlotte's course average in chemistry class is the average of the best five of her six hourly test scores. Going into finals week, Charlotte has scores of 88, 84, 84, 89, and 72. How much, at minimum, must Charlotte score on her sixth test in order to make an average of 85 or better for the term?
Charlotte is already assured of a course average of at least 85 for the term.
If Charlotte does not take the sixth test, she will receive the average of her first five tests - this is
Charlotte is not assured of an 85 or better, so she must take the test to achieve this.
Let 


Since Charlotte wants an average of 85 or better, we solve this inequality:
Her sixth test must be 80, at minimum.
Example Question #24 : Calculating Arithmetic Mean
Consider the data set
For the set to have mean greater than or equal to 50, what must hold true about 

One must be greater than 94; the other must be less than 94.
One must be greater than 47; the other must be less than 47.
Their sum must be greater than or equal to 94.
Their sum must be greater than or equal to 47.
Each must be greater than or equal to 47.
Their sum must be greater than or equal to 47.
Divide the sum of the eight elements by 8 to get the mean, which must be greater than or equal to 50:
This is all that is needed for the set to have mean 50.
Example Question #25 : Calculating Arithmetic Mean
What is the mean for the following data set:
The mean is the average of the data set. There are 
Example Question #21 : Arithmetic Mean
What is the mean for the following set:
The mean is the average of all of the numbers:
Example Question #27 : Calculating Arithmetic Mean
Consider the data set
What is its mean?
Add the ten elements and divide the sum by 10. The mean is
Example Question #28 : Calculating Arithmetic Mean
A gymnastics meet has seven judges. After each routine, each judge assigns a merit-based score from 0 to 10. To guard against bias, a contestant's score for the routine is the mean of all the judges' scores except for the highest and the lowest.
On one of Sarah's routines, each of the following judges scores her as follows:
What is Sarah's score?
Ellis and Jones gave Sarah the highest and lowest scores, respectively, so her score will be the mean of the other five:
Example Question #29 : Calculating Arithmetic Mean
Find 

The formula for the arithmetic mean is:
Mean=
We can then write:
All GMAT Math Resources




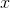

















































![\left [ 1+ \left ( -2 \right )+3 +\left ( -4 \right )+5+ \left ( -6 \right )+7+ \left ( -8 \right )+9+\left ( -10 \right ) \right ] \div 10](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/166661/gif.latex)






















