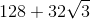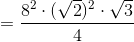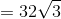The volume of a pyramid can be calculated using the formula

, 

where  is the area of the base and  is the height. The base of the pyramid in question is a square; if we let its sidelength be , this base will be , and the volume formula will be

Setting  and :

or

.

The square base of the pyramid has four sides with length 15 inches, making its perimeter four times that, or 60 inches. The slant height is 

 inches.

Therefore, the area of the base is  square inches.

Each of the four lateral triangles has area  square inches.

The total surface area is  square inches.

The tetrahedron looks like this:

 is the origin and  are the other three points, which are 60 units away from the origin on each of the three (perpendicular) axes.

The bottom, front, and left faces are each right triangles whose legs each measure 60. Each face has area

.

The remaining face has three edges each a hypotenuse of one of three congruent right triangles, so its sides are congruent, and it is an equilateral triangle. Its sidelength can be found via the 45-45-90 Theorem to be , so its area is

The total area is 

As shown in the diagram below, a regular tetrahedron has six congruent edges, so each has length :

The area of one face is the area of an equilateral triangle with sidelength 20, which is

The total surface area is four times this, or .

The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula

There are four congruent faces, so the total surface area is

Since , the surface area of the tetrahedron is

A tetrahedron looks like this:

The tetrahedron has six edges, and in a regular tetrahedron, they are congruent, so each edge has length .

The area of one face of the tetrahedron, it being an equilateral triangle, can be calulated using the formula

There are four congruent faces, so the total surface area is

Since , the surface area of the tetrahedron is

Three of the faces of the tetrahedron are isosceles right triangles with legs of length 8, and, subsequently, by the 45-45-90 Theorem, hypotenuses of length . The fourth face, consequently, is an equilateral triangle with three sides of length .

Each of the three right triangle faces has area equal to half the product of its legs , which is

.

The equilateral face has as its area 

The sum of the areas of the faces is 

Three of the surfaces of the tetrahedron - , , and   - are isosceles right triangles with hypotenuse 30, so by the 45-45-90 Theorem, each leg measures this length divided by , or

 .

The area of each of these triangles is half the product of its legs, so each area is 

Also, the legs are of the same measure among the triangles, the hypotenuses are as well, so the fourth surface  is an equilateral triangle. Its sidelength is , so we use the equilateral triangle area formula to calculate its area:

Add the areas of the faces:

The base is an equilateral triangle with sidelength 12, so its area can be calculated as follows:

.

Each of the three other faces is congruent, with base 12. The area of each is the product of its base and its height. To find the common height, we examine , which, since  is an altitude of isosceles , is a right triangle with hypotenuse of length 18 and one leg of length . We can find  using the Pythagorean Theorem:

The area of  is half the product of this height and the base:

All three lateral faces have this area.

Now add the areas of the four faces:

The surface area formula can be used to find the length of each edge of the cube:

Three faces of the tetrahedron - ,  ,  - are right triangles with legs of length 8, so the area of each is half the product of the lengths of their legs:

.

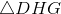
Each triangle is isosceles, so, by the 45-45-90 Theorem, each of their hypotentuses measures  times a leg, or .  is therefore an equilateral triangle with sidelenghth . Its area can be found as follows:

The total surface area is