All GED Math Resources
Example Questions
Example Question #251 : Geometry And Graphs
If a triangle is isosceles, and the vertex angle is 100 degrees, what must be another angle?
The isosceles triangle has two congruent sides and two congruent angles.
The interior angles will sum to 180 degrees.
Let the unknown angles be 
Divide by 2 on both sides.
The answer is:
Example Question #251 : Geometry And Graphs

Figure NOT drawn to scale.
Refer to the above diagram. Evaluate



Since the measures of the interior angles of a triangle total 
Substitute 




Subtract 
Multiply both sides by 




Substitute and add:

Example Question #19 : Angles And Triangles
For an isosceles triangle, if the vertex angle is measured 30 degrees, what must a base angle equal?
An isosceles has two equivalent base angles. We can set up an equation such that both angles with the vertex angle add up to 180 degrees.
Solve for 
Divide by 2 on both sides.
The answer is:
Example Question #20 : Angles And Triangles
The figure below is what type of triangle?

Right
Isosceles
Scalene
Equiangular
Scalene
Start by figuring out the degree measurements of each angle.
Since we know that the angles of a triangle must add up to 
Solve for 
Now, we know the measure of the angles:
Since each angle of the triangle is different, this means the the legs of the triangle must also be different. Thus, this is a scalene triangle.
Example Question #251 : 2 Dimensional Geometry
Which of the following can be the measures of the three angles of an isosceles triangle?
By the Isosceles Triangle Theorem, an isosceles triangle - a triangle with at least two sides of equal length - must have at least two angles of equal degree measure. The choice 
Also, the degree measures must total 




The last group is the correct choice.
Example Question #21 : Angles And Triangles
A triangle has one angle measure of 







For all triangles, the sum of the three angles is equal to 




Example Question #251 : 2 Dimensional Geometry
If one angle of an isosceles triangle measures 120, what are the other two angle measures?
First we need to recall that whenever we add up all 3 angles of any given triangle, the sum will always be 
In an isosceles triangle two of the angles are congruent. Since we are told that one of the angles of our triangle is 
We need to subtract 120 from 180 to find the remainder of the triangle which is
Since we are working with an isosceles triangle, we know that the remaining two angles are going to be congruent. To find the degree of the angles we simply divide 60 by 2. Our answer is; both angles are
Example Question #251 : Geometry And Graphs
Which of the following statements is not a consequence of the statement







However, similar triangles need not have congruent corresponding sides. Therefore, it does not necessarily follow that 
Example Question #252 : Geometry And Graphs
Which of the following statements follows from the statement 
The similarity of two triangles implies nothing about the relationship of two angles of the same triangle. Therefore, 
The similarity of two triangles implies that corresponding angles between the triangles are congruent. However, because of the positions of the letters, 






Similarity of two triangles does not imply any congruence between sides of the triangles, so 
Similarity of triangles implies that corresponding sides are in proportion. 






Example Question #1 : Similar Triangles And Proportions
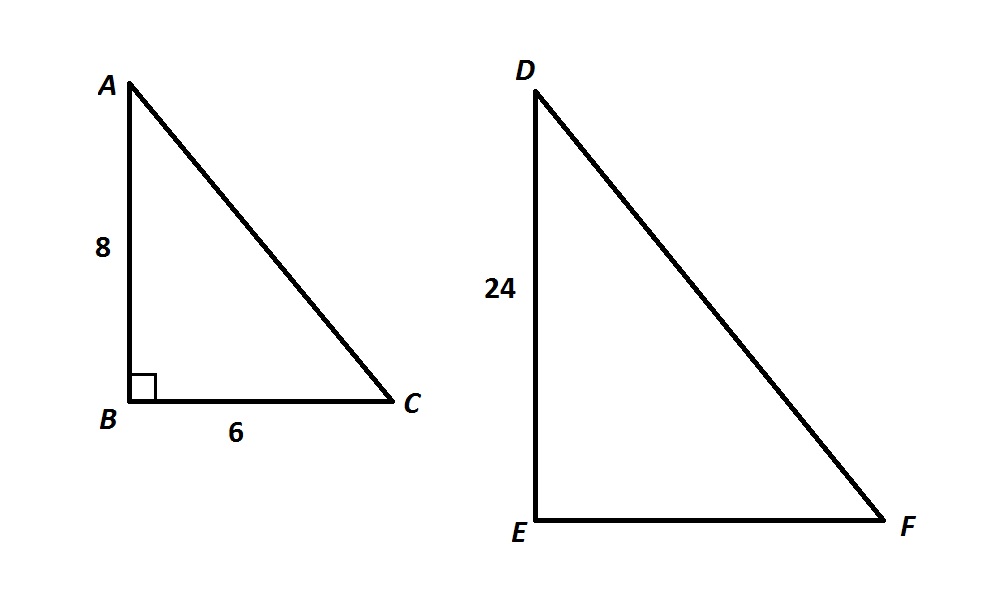
Note: Figure NOT drawn to scale.
Refer to the above diagram. If 

Suppose 
Corresponding angles of similar triangles are congruent, so 



Corresponding sides of similar triangles are in proportion. Since

the similarity ratio of 

By the Pythagorean Theorem, since 



But 

All GED Math Resources



































































