We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

GED Math : 2-Dimensional Geometry

Study concepts, example questions & explanations for GED Math

Create An Account

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #51 : Complementary Angles

Find the the measure of angle B if it is complement of angle A:

$m\angle A=18^{o}$

Possible Answers:

$m\angle B=82^{o}$

$m\angle B=36^{o}$

$m\angle B=136^{o}$

$m\angle B=72^{o}$

Correct answer:

$m\angle B=72^{o}$

Explanation:

If two angles are complementary, that means the sum of their degrees of measure will add up to 90. In order to find the measure of angle B, subtract angle A from 90 like shown:

$m\angle B=90^{o}-18^{o}=72^{o}$

This gives us a final answer of 72 degrees for angle B.

Report an Error

Example Question #52 : Complementary Angles

Find the the measure of angle B if it is complement of angle A:

$m\angle A=87^{o}$

Possible Answers:

$m\angle B=3^{o}$

$m\angle B=72^{o}$

$m\angle B=112^{o}$

$m\angle B=13^{o}$

Correct answer:

$m\angle B=3^{o}$

Explanation:

If two angles are complementary, that means the sum of their degrees of measure will add up to 90. In order to find the measure of angle B, subtract angle A from 90 like shown:

$m\angle B=90^{o}-87^{o}=3^{o}$

This gives us a final answer of 3 degrees for angle B.

Report an Error

Example Question #53 : Complementary Angles

Find the the measure of angle B if it is complement of angle A:

$m\angle A=39^{o}$

Possible Answers:

$m\angle B=123^{o}$

$m\angle B=3^{o}$

$m\angle B=11^{o}$

$m\angle B=51^{o}$

Correct answer:

$m\angle B=51^{o}$

Explanation:

If two angles are complementary, that means the sum of their degrees of measure will add up to 90. In order to find the measure of angle B, subtract angle A from 90 like shown:

$m\angle B=90^{o}-39^{o}=51^{o}$

This gives us a final answer of 51 degrees for angle B.

Report an Error

Example Question #54 : Complementary Angles

Find the the measure of angle B if it is complement of angle A:

$m\angle A=53^{o}$

Possible Answers:

$m\angle B=37^{o}$

$m\angle B=116^{o}$

$m\angle B=27^{o}$

$m\angle B=11^{o}$

Correct answer:

$m\angle B=37^{o}$

Explanation:

If two angles are complementary, that means the sum of their degrees of measure will add up to 90. In order to find the measure of angle B, subtract angle A from 90 like shown:

$m\angle B=90^{o}-53^{o}=37^{o}$

This gives us a final answer of 37 degrees for angle B.

Report an Error

Example Question #55 : Complementary Angles

Find the the measure of angle B if it is complement of angle A:

$m\angle A=9^{o}$

Possible Answers:

$m\angle B=12^{o}$

$m\angle B=85^{o}$

$m\angle B=116^{o}$

$m\angle B=81^{o}$

Correct answer:

$m\angle B=81^{o}$

Explanation:

If two angles are complementary, that means the sum of their degrees of measure will add up to 90. In order to find the measure of angle B, subtract angle A from 90 like shown:

$m\angle B=90^{o}-9^{o}=81^{o}$

This gives us a final answer of 81 degrees for angle B.

Report an Error

Example Question #56 : Angle Geometry

If an angle measures 23.5 degrees, find the measurement of the other angle such that the two angles are complementary.

Possible Answers:

66.5

65.5

75.5

67.5

Correct answer:

66.5

Explanation:

Two angles are classified as complementary if an only if the sum of the angles equals to exactly 90 degrees.

Since we know the measurement of one angle, and we know the rule about complementary angles, let's find the other angle:

The other angle is simply the total sum of both angles minus the given angle.
The total sum of the angles is , and the given angle is 23.5 .

So, we will subtract 23.5 from .

Other angle= 90-23.5=66.5

The other angle has a measurement of 66.5 degrees.

Report an Error

Example Question #1 : Supplementary Angles

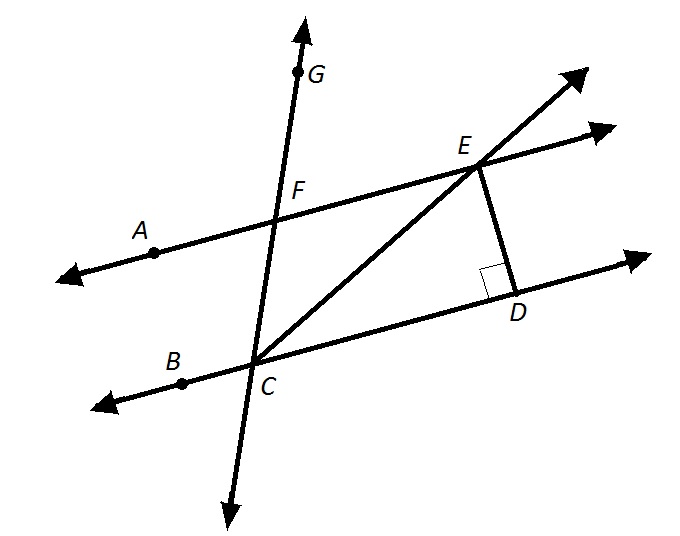
Thingy

Refer to the above diagram.

$\overleftrightarrow{AE} ||\overleftrightarrow{BD}$ ; $m \angle BCE = 136^{\circ }$ . Evaluate $m \angle CED$ .

Possible Answers:

$54 ^{\circ }$

$56 ^{\circ }$

$46 ^{\circ }$

$44 ^{\circ }$

Correct answer:

$46 ^{\circ }$

Explanation:

$\angle BCE$ and $\angle ECD$ form a linear pair, so they are supplementary - that is, their degree measures total $180^{\circ }$ , so

$m \angle BCE + m\angle ECD =180^{\circ }$

$136^{\circ } + m\angle ECD =180^{\circ }$

$m\angle ECD =180^{\circ } - 136 ^{\circ } = 44^{\circ }$

$m \angle CED$ and $\angle ECD$ are acute angles of right triangle $\Delta ECD$ , so they are complementary - that is, their degree measures total $90^{\circ }$ , so

$m \angle CED + m\angle ECD =90^{\circ }$

$m \angle CED + 44 ^{\circ } =90^{\circ }$

$m \angle CED =90^{\circ } - 44 ^{\circ } = 46 ^{\circ }$

Report an Error

Example Question #487 : 2 Dimensional Geometry

Angles A, B, and C are supplementary. The measure of angle A is 5x + 15 . The measure of angle B is 2x + 25 . The measure for angle C is 2x + 14 . Find the value of .

Possible Answers:

x = 24

x = 16

x = -2

x = 10

x= 14

Correct answer:

x= 14

Explanation:

Since angles A, B, and C are supplementary, their measures add up to equal 180 degrees. Therefore we can set up the equation as such:

A + B + C =180

-or-

5x + 15 + 2x + 25 + 2x + 15 = 180

Combine like terms and solve for :

9x + 54 = 180

9x = 126

x = 14

Report an Error

Example Question #488 : 2 Dimensional Geometry

Angles A and B are supplementary. The measure of angle A is 17x + 20 . The measure of Angle B is -2x + 10 . Find the value of .

Possible Answers:

x = -10

No solution

x = 10

x = 5

x = 15

Correct answer:

x = 10

Explanation:

Since angles A and B are supplementary, thier measurements add up to equal 180 degrees. Therefore we can set up our equation like such:

A + B = 180

-or-

17x + 20 + -2x + 10 = 180

Combine like terms and solve for :

15x + 30 = 180

15x = 150

x = 10

Report an Error

Example Question #489 : 2 Dimensional Geometry

Angles A, B, and C are supplementary. The measure of angle A is 10x + 4 . The measure of angle B is 5x - 6 . The measure for angle C = 3x + 2 . What are the measure for the three angles?

Possible Answers:

$Angle A = 44^{\circ}$

$Angle B = 32^{\circ}$

$Angle C = 104^{\circ}$

$Angle A = 120^{\circ}$

$Angle B = 40^{\circ}$

$Angle C = 20^{\circ}$

No solution

$Angle A = 104^{\circ}$

$Angle B = 44^{\circ}$

$Angle C = 32^{\circ}$

$Angle A = 114^{\circ}$

$Anbgle B = 32^{\circ}$

$Angle C = 36^{\circ}$

Correct answer:

$Angle A = 104^{\circ}$

$Angle B = 44^{\circ}$

$Angle C = 32^{\circ}$

Explanation:

Since angles A, B, and C are supplementary, their measures add up to equal 180 degrees. Therefore we can set up an equation as such:

A + B + C = 180

-or-

10x + 4 + 5x - 6 + 3x + 2 = 180

Combine like terms and solve for x:

18x = 180

x = 10

Plug back into the three angle measurements:

Angle A = 10(10) + 4

Angle A = 100 + 4 4

Angle A = 104

Angle B = 5(10) - 6

Angle B = 50 -6

Angle B = 46

Angle C = 3(10) + 2

Angle C = 30 + 2

Angle C = 32

Report an Error

View Tutors

Simon
Certified Tutor

University of Cambridge, Bachelor in Arts, General Literature. University of Wolverhampton, Doctor of Philosophy, History.

View Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

View Tutors

Damali
Certified Tutor

St. Mary's University, Bachelor in Arts, English.

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Math Tutors in Boston, SAT Tutors in Denver, LSAT Tutors in Miami, GRE Tutors in San Diego, MCAT Tutors in Seattle, Biology Tutors in Washington DC, Statistics Tutors in Dallas Fort Worth, French Tutors in Philadelphia, Spanish Tutors in Atlanta, English Tutors in San Francisco-Bay Area

Popular Courses & Classes

Spanish Courses & Classes in Miami, ACT Courses & Classes in Los Angeles, GMAT Courses & Classes in Miami, MCAT Courses & Classes in Boston, GRE Courses & Classes in Denver, ACT Courses & Classes in Seattle, SAT Courses & Classes in Philadelphia, SAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in New York City

Popular Test Prep

ISEE Test Prep in Boston, ACT Test Prep in Seattle, MCAT Test Prep in Denver, SSAT Test Prep in Los Angeles, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Miami, LSAT Test Prep in Seattle, MCAT Test Prep in Phoenix, ISEE Test Prep in Chicago, SSAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GED Math : 2-Dimensional Geometry

Study concepts, example questions & explanations for GED Math

All GED Math Resources

Example Questions

Example Question #51 : Complementary Angles

Example Question #52 : Complementary Angles

Example Question #53 : Complementary Angles

Example Question #54 : Complementary Angles

Example Question #55 : Complementary Angles

Example Question #56 : Angle Geometry

Example Question #1 : Supplementary Angles

Example Question #487 : 2 Dimensional Geometry

Example Question #488 : 2 Dimensional Geometry

Example Question #489 : 2 Dimensional Geometry

All GED Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: