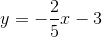Since we are asked to find the perimeter of the triangle, we will need to use the distance formula to find the length of each side. Recall the distance formula:

Start by finding the distance between the points :

Next, find the distance between .

Then, find the distance between .

Finally, add up the lengths of each side to find the perimeter of the triangle.

Find the distance between the points  and .

To find the distance between two points, we will use distance formula (clever name). Distance formula can be thought of as a modified Pythagorean Theorem. What distance formula does is essentially treats our two points as the ends of a hypotenuse on a right triangle, then uses the two side lengths to find the hypotenuse.

Distance formula:

Pythagorean Theorem

If the connection isn't clear, don't worry, we can still solve for distance.

So our answer is 407

Recall the distance formula:

Plug in the given points to find the distance between them.

The distance between those points is .

Find the length of the line connecting the following points.

To find the length of a line, use distance formula.

What we are really doing is making a right triangle and using Pythagorean Theorem to find the hypotenuse. 

Let's plug in our points and find the distance!

So our answer is 110

Remember that you can consider your two points as:

 and 

From this, remember that the distance formula is:

Now, for your data, this is:

or

You can simplify this value a little. Identify the prime factors of  and move any number that appears in a pair of factors from the interior to the exterior of the square root symbol:

Remember that you can consider your two points as:

 and 

From this, remember that the distance formula is:

Now, for your data, this will look like the following.  Be very careful with the negative signs:

or

 is only factorable into  and ; therefore, your answer is in its final form already.

The -intercept will be a point  for some value . We use the slope formula

,

setting ,

and solving for :

The -intercept is .

The -intercept will be the point  for some value . We use the slope formula

,

setting ,

and solving for :

The -intercept is .

The inequality symbol of the statement 

allows for the two quantities to be equal, so the line of the equation

must be part of the graph of the inequality. Therefore, we must select one of the choices with a solid line. Of the two such choices, we can determine which one to select by choosing a test point on one side of the line and substituting the coordinates in the inequality.

The easiest point to select is the origin, or .  Set  in the inequality:

This is false, so we want the choice that does not include the point . The correct choice is the graph:

When rolling a die, the following outcomes are possible:

Of the outcomes, outcomes are or greater. Therefore,