Call Now to Set Up Tutoring:

(888) 888-0446

GED Math : Angles

Study concepts, example questions & explanations for GED Math

Create An Account

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Angles

What is the measure of each angle of a regular octagon?

Possible Answers:

$150 ^{\circ }$

$120^{\circ }$

$135 ^{\circ }$

$140 ^{\circ }$

$125 ^{\circ }$

Correct answer:

$135 ^{\circ }$

Explanation:

The sum of the degree measures of the angles of a polygon with sides is 180(N-2 ) . Since an octagon has eight sides, substitute N = 8 to get:

$180(8-2 ) = 180 \times6 = 1,080$

Each angle of a regular polygon has equal measure, so divide this by 8 to get the measure of one angle:

$1,080 \div 8 = 135$ , the degree measure of one angle.

Report an Error

Example Question #1 : Angles

Give the measure of each interior angle of a regular 72-sided polygon.

Possible Answers:

$175^{\circ }$

$170^{\circ }$

$172^{\circ }$

$178^{\circ }$

Correct answer:

$175^{\circ }$

Explanation:

A regular polygon with sides has interior angles of measure $\frac{(n-2)180^{\circ }}{n}$ each. Substitute 72 for .

$\frac{(72-2)180^{\circ }}{72}= \frac{70 \times 180^{\circ }}{72} = 175^{\circ }$

Report an Error

Example Question #1 : Angles

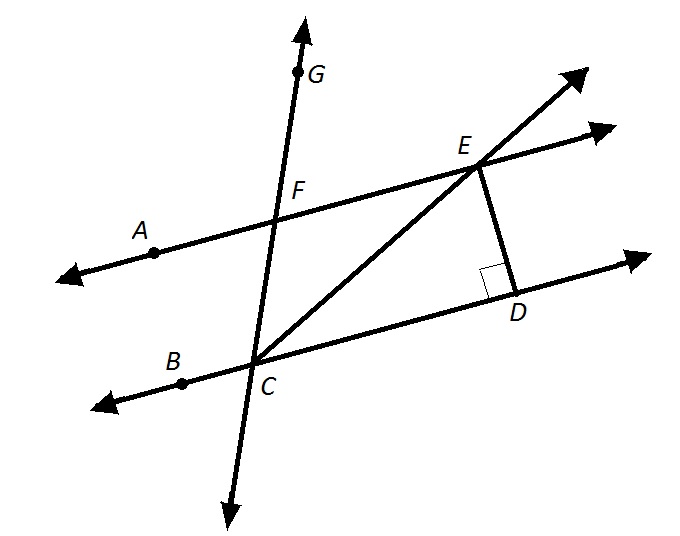
Thingy

Refer to the above diagram.

Which of these is a valid alternative name for $\angle FEC$ ?

Possible Answers:

$\angle CEA$

$\angle E$

$\angle GCE$

$\angle GFE$

Correct answer:

$\angle CEA$

Explanation:

When naming an angle after three points, the middle letter must be its vertex, or the point at which its sides meet - this is . The other two letters must refer to points on its two sides. Therefore, $\angle FEC$ includes on one side, making one of its sides $\overrightarrow{EF}$ , and on the other, making the other side $\overrightarrow{EC}$ .

An alternative name for this angle must be one of two things:

It can be named only after its vertex - that is, $\angle E$ - but only if there is no ambiguity as to which angle is being named. Since more than one angle in the diagram has vertex , $\angle E$ is not a correct choice.

It can be named after three points. Again, the middle letter must be vertex , so we can throw out $\angle GCE$ and $\angle GFE$ .

The only possible choice is $\angle CEA$ .

Report an Error

Example Question #3 : Angles

Hexagon

Note: Figure NOT drawn to scale.

The above hexagon is regular. What is ?

Possible Answers:

x =75

x=70

x=80

x= 65

Correct answer:

x =75

Explanation:

Two of the angles of the quadrilateral formed are angles of a regular hexagon, so each measures

$\frac{180^{\circ } (6-2)}{6}= 120^{\circ }$ .

The four angles of the quadrilateral are $120 ^{\circ }, 120^{\circ }, 45^{\circ }, x^{\circ }$ . Their sum is $360^{\circ }$ , so we can set up an equation and solve for :

x + 120 + 120 + 45 =360

x + 285 =360

x = 75

Report an Error

Example Question #3 : Angles

Octagon

The above octagon is regular. What is ?

Possible Answers:

y = 50

y = 65

y = 60

y = 55

Correct answer:

y = 55

Explanation:

Three of the angles of the pentagon formed are angles of a regular octagon, so each measures

$\frac{180^{\circ } (8-2)}{8}= 135^{\circ }$ .

The five angles of the pentagon are $135^{\circ }, 135^{\circ }, 135^{\circ }, 80^{\circ }, y^{\circ }$ . Their sum is $180^{\circ } (5-3) = 540^{\circ }$ , so we can set up an equation and solve for :

y+ 135+ 135 + 135 +80 = 540

y+ 485= 540

y = 55

Report an Error

Example Question #2 : Angles

Pentagon

Note: Figure NOT drawn to scale.

Refer to the above figure. $\Delta OKR$ is equilateral and Pentagon KLMNO is regular.

Evaluate $m \angle NRO$ .

Possible Answers:

$48^{\circ }$

$72^{\circ }$

$66^{\circ }$

$54 ^{\circ }$

Correct answer:

$66^{\circ }$

Explanation:

First, we find $m \angle NOR$ .

By angle addition,

$m \angle NOR + m \angle ROK = m \angle NOK$ .

$\angle NOK$ is an angle of a regular pentagon and has measure $\frac{180^{\circ}\times (5-2)}{5} = 108 ^{\circ}$ .

$\angle ROK$ , as an angle of an equilateral triangle, has measure $60 ^{\circ }$ .

$m \angle NOR + 60 ^{\circ }= 108 ^{\circ }$

$m \angle NOR = 48 ^{\circ }$

$\Delta OKR$ is equilateral, so $\overline{OR} \cong \overline{OK}$ ; Pentagon KLMNO is regular, so $\overline{OK} \cong \overline{NO}$ . Therefore, $\overline{OR} \cong \overline{ON}$ , and by the Isosceles Triangle Theorem, $m \angle NRO = m \angle RNO$ .

The degree measures of three angles of a triangle total $180 ^{\circ }$ , so:

$m \angle NRO + m \angle RNO + m \angle NOR = 180^{\circ }$

$m \angle NRO + m \angle NRO + 48^{\circ } = 180^{\circ }$

$2 m \angle NRO + 48^{\circ } = 180^{\circ }$

$2 m \angle NRO = 132^{\circ }$

$m \angle NRO = 66^{\circ }$

Report an Error

Example Question #4 : Angles

Pentagon_1

Refer to the above figure, which shows Square OPQK and regular Pentagon KLMNO .

Evaluate $m \angle NOQ$ .

Possible Answers:

$165^{\circ}$

$153^{\circ}$

$135^{\circ}$

$168^{\circ}$

Correct answer:

$153^{\circ}$

Explanation:

By angle addition,

$m \angle NOQ = m \angle NOK + m \angle KOQ$ .

$\angle NOK$ is an angle of a regular pentagon and has measure $\frac{180^{\circ}\times (5-2)}{5} = 108 ^{\circ}$ .

$\angle KOQ$ is one of two acute angles of isosceles right triangle $\Delta KOQ$ , so $m \angle KOQ = 45^{\circ }$ .

$m \angle NOQ = 108^{\circ } + 45^{\circ } = 153^{\circ }$

Report an Error

Example Question #5 : Angles

Thingy_2

Refer to the above figure. $\Delta OKR$ is equilateral, and Quadrilateral OPQK is a square.

Evaluate $m \angle ROP$ .

Possible Answers:

$150 ^{\circ }$

$140 ^{\circ }$

$168^{ \circ }$

$135^{\circ }$

Correct answer:

$150 ^{\circ }$

Explanation:

By angle addition,

$m \angle ROP = m \angle ROK + m \angle KOP$ .

$\angle ROK$ , as an angle of an equilateral triangle, has measure $60 ^{\circ }$ .

$\angle KOP$ , as an angle of a square, has measure $90 ^{\circ }$ .

Therefore,

$m \angle ROP = 60 ^{\circ } + 90^{\circ } = 150 ^{\circ }$ .

Report an Error

Example Question #31 : Other Shapes

Give the number of sides of a regular polygon whose interior angles have measure $170^{\circ }$ .

Possible Answers:

Correct answer:

Explanation:

The easiest way to solve this is to look at the exterior angles, each of which have measure $(180-170)^{\circ } = 10^{\circ }$ . Since each exterior angle of a regular polygon with sides is $\frac{360}{N}$ , we solve for in the following equation:

$\frac{360}{N} = 10$

$\frac{360}{N} \cdot \frac{N }{10} = 10 \cdot \frac{N }{10}$

36 = N

The polygon has 36 sides.

Report an Error

Example Question #3 : Angles

Three consecutive even angles add up to 180 . What must be the value of the second largest angle?

Possible Answers:

Correct answer:

Explanation:

Let be an even angle. The next consecutive even values are x+2, x+4 .

Set up an equation such that all angles added equal to 180.

x+(x+2)+(x+4) = 180

3x+6 = 180

3x=174

Divide by three on both sides.

$\frac{3x}{3}=\frac{174}{3}$

x=58

The second largest angle is x+2 .

Substitute the value of in to the expression.

58+2 = 60

The answer is:

Report an Error

View Tutors

Margaret
Certified Tutor

Smith College, Bachelor of Science, Biological and Physical Sciences.

View Tutors

Samir
Certified Tutor

University of South Florida-Main Campus, Master of Fine Arts, Studio Arts.

View Tutors

Grace
Certified Tutor

University of Massachusetts-Dartmouth, Bachelor of Education, Portuguese. University of Massachusetts-Dartmouth, Masters in B...

All GED Math Resources

4 Diagnostic Tests 263 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ISEE Tutors in New York City, Physics Tutors in Seattle, MCAT Tutors in Atlanta, Chemistry Tutors in Los Angeles, MCAT Tutors in Miami, GMAT Tutors in Seattle, ISEE Tutors in Seattle, French Tutors in Philadelphia, ACT Tutors in Boston, ISEE Tutors in Denver

Popular Courses & Classes

SSAT Courses & Classes in Miami, SAT Courses & Classes in Houston, ACT Courses & Classes in Boston, GMAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in Washington DC, GRE Courses & Classes in Miami, SAT Courses & Classes in San Diego, GRE Courses & Classes in Atlanta, LSAT Courses & Classes in Atlanta, ISEE Courses & Classes in Miami

Popular Test Prep

ACT Test Prep in Boston, GMAT Test Prep in Miami, SSAT Test Prep in Miami, GRE Test Prep in Boston, MCAT Test Prep in San Francisco-Bay Area, ACT Test Prep in Seattle, ISEE Test Prep in Miami, GMAT Test Prep in Philadelphia, SSAT Test Prep in Boston, SAT Test Prep in Phoenix

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

GED Math : Angles

Study concepts, example questions & explanations for GED Math

All GED Math Resources

Example Questions

Example Question #1 : Angles

Example Question #1 : Angles

Example Question #1 : Angles

Example Question #3 : Angles

Example Question #3 : Angles

Example Question #2 : Angles

Example Question #4 : Angles

Example Question #5 : Angles

Example Question #31 : Other Shapes

Example Question #3 : Angles

All GED Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: