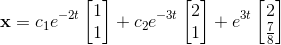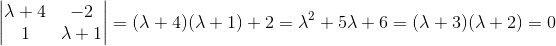First, we will need the complementary solution, and a fundamental matrix for the homogeneous system. Thus, we find the characteristic equation of the matrix given.

Using , we then find the eigenvectors by solving for the eigenspace.

This has solutions , or . So a suitable eigenvector is simply .

Repeating for ,

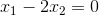
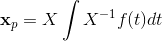
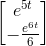
This has solutions , and thus a suitable eigenvector is . Thus, our complementary solution is  and our fundamental matrix (though in this case, not the matrix exponential) is . Variation of parameters tells us that the particular solution is given by , so first we find  using the inverse rule for 2x2 matrices. Thus, . Plugging in, we have . So  .

Finishing up, we have .

Adding the particular solution to the homogeneous, we get a final general solution of 

Given the matrix,

and using the definition of matrix exponential, 

calculate 

Therefore 

First we find our eigenvalues by finding the characteristic equation, which is the determinant of  (or ). Expansion down column one yields

Simplifying and factoring out a , we have

So our eigenvalues are 

To find the eigenvectors, we find the basis for the null space of  for each lambda.

lambda = -1

Adding row 1 to row 3 and placing into row 3, dividing row two by 6, and swapping rows two and 1 gives us our reduced row echelon form. For our purposes, it suffices just to do the first step and look at the resulting system.

So that 

Which has solutions  . Thus, a clean eigenvector here would be  

For lambda = 4, we have 

Step 1: Add row 3 to row 1.

Step 2: Add 3 row 3 to row 2

Step 3: Add -6/5 row 1 in to row 2. Swap and divide as necessary to get proper pivots.

This gives us

So that 

Which has solutions  . Thus, a clean eigenvector here would be  .

As we only ended up with two eigenvectors, we'll need to grab a generalized eigenvector as well. To do this, we will solve

(for lambda = 1, and we set it equal to the negation of our eigenvector for 1.)

This gives us

And the steps to solve this are identical to the steps to solving for the eigenvector for -1. Following them once more, and further reducing, we get.

Solving the system, our generalized eigenvector is given by . Decomposing into the Jordan matrix gives us

,

When we exponentiate this in the above form, we only need to find the matrix exponential of the Jordan matrix. This is done by exponentiating the entries on the main diagonal, and making the entries on the super diagonals of each Jordan block powers of t over the proper factorials. Thus, the matrix exponential is given by

From here, it would just be a matter of inverting and multiplying together -- daunting algebraically, but conceptually quite easy.

Note: In the final form above, anything with the same entries, but the columns switched is okay. I.e., it's okay to have the first eigenvector in the last column of the last two matrices, and  be in the lower right hand corner of the second matrix.

First we find our eigenvalues by finding the characteristic equation, which is the determinant of  (or ).

Thus, we have eigenvalues of 4 and 2. Solving for the eigenvectors by finding the bases of the eigenspaces, we have

lambda = 4

Adding Row1 into Row 2, we're left with

So that 

And have an eigenvector of .

For lambda = 2, we have 

Adding -1 Row 1 into Row 2, we have

So that 

and  is an eigenvector.

Constructing our diagonalized matrix, we have 

Using the formula for calculating the inverses of 2x2 matrices, we have

To calculate the matrix exponential, we can just find the matrix exponential of  and multiply  and  back in. So .

 is just found by taking the entries on the diagonal and exponentiating. Thus, 

Multiplying together, we get

Given the matrix,

and using the definition of matrix exponential, 

calculate 

Therefore 

To get the matrix exponential, we will have to diagonalize the matrix, which requires us to find the eigenvalues and eigenvectors. Thus, we have

Using , we then find the eigenvectors by solving for the eigenspace.

This has solutions , or . So a suitable eigenvector is simply .

Repeating for ,

This has solutions , and thus a suitable eigenvector is .

Thus, we have , , and using the inverse formula for 2x2 matrices, . Now we just take the matrix exponential of  and multiply the three matrices back together. Thus,

Multiplying these out yields

The auxiliary equation is

The roots are

Our solution is