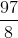Call Now to Set Up Tutoring:

(888) 888-0446

Differential Equations : Numerical Solutions of Ordinary Differential Equations

Study concepts, example questions & explanations for Differential Equations

Create An Account

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : Euler Method

Use Euler's Method to calculate the approximation of y(0.2) where y(x) is the solution of the initial-value problem that is as follows.

y''+xy'+y=0

y(0)=2, y'(0)=3

Possible Answers:

$y(0.2)\approx2.542$

$y(0.2)\approx2.5$

$y(0.2)\approx2.458$

$y(0.2)\approx2.58$

$y(0.2)\approx2.584$

Correct answer:

$y(0.2)\approx2.58$

Explanation:

Using Euler's Method for the function

y''+xy'+y=0

y(0)=2, y'(0)=3

first make the substitution of

$\\y'=u \\u'=-xu-y$

therefore

$\\y_{n+1}=y_n+hu_n \\u_{n+1}=u_n+h[-x_nu_n-y_n]$

where represents the step size.

Let

$\\h=0.1 \\y_0=2 \\u_0=3$

Substitute these values into the previous formulas and continue in this fashion until the approximation for y(0.2) is found.

$\\y_1=y_0+(0.1)u_0=2+(0.1)(3)=2.3 \\u_1=u_0+(0.1)[-x_0u_0-y_0]=3+(0.1)[0(2)-2]=2.8 \\y_2=y_1+(0.1)u_1=2.3+(0.1)(2.8)=2.58 \\u_2=u_1+(0.1)[-x_1u_1-y_1]=2.8+(0.1)[-0.1(2.8)-2.3]=2.542$

Therefore,

$y(0.2)\approx2.58$

Report an Error

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Approximate $y(\pi)$ for $y = \cos(y)(2-y)$ with time steps $h = \frac{\pi}{4}$ and y(0) = 0 .

Possible Answers:

$\frac{5\pi}{8}$

$\frac{\pi}{4}$

$\frac{\pi}{2}$

$\frac{3\pi}{2}$

Correct answer:

$\frac{\pi}{2}$

Explanation:

Approximate $y(\pi)$ for $y = \cos(y)(2-y)$ with time steps $h = \frac{\pi}{4}$ and y(0) = 0 .

The formula for Euler approximations $\mu(t+h) = \mu (t) + h \cdot f(t, \mu(t))$ .

Plugging in, we have

$\mu(\frac{\pi}{4}) = \mu (0) + \frac{\pi}{4}f(0, \mu(0)) = 0 + \frac{\pi}{4}(\cos(0)(2-0)) = \frac{\pi}{2}$

$\mu(\frac{\pi}{2}) = \mu (\frac{\pi}{4}) + \frac{\pi}{4}f(\frac{\pi}{4}, \mu(\frac{\pi}{4})) = \frac{\pi}{2} + \frac{\pi}{4}(\cos(\frac{\pi}{2})(2-\frac{\pi}{2})) = \frac{\pi}{2} + 0 = \frac{\pi}{2}$

Here we can see that we've gotten trapped on a horizontal tangent (a failing of Euler's method when using larger time steps). As the function is not dependent on t, we will continue to move in a horizontal line for the rest of our Euler approximations. Thus $\mu(\pi) = \frac{\pi}{2} \approx y(\pi)$ .

Report an Error

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Use Euler's Method to calculate the approximation of y(0.2) where y(x) is the solution of the initial-value problem that is as follows.

y''+xy'+y=0

y(0)=2, y'(0)=3

Possible Answers:

$y(0.2)\approx2.542$

$y(0.2)\approx2.458$

$y(0.2)\approx2.584$

$y(0.2)\approx2.5$

$y(0.2)\approx2.58$

Correct answer:

$y(0.2)\approx2.58$

Explanation:

Using Euler's Method for the function

y''+xy'+y=0

y(0)=2, y'(0)=3

first make the substitution of

$\\y'=u \\u'=-xu-y$

therefore

$\\y_{n+1}=y_n+hu_n \\u_{n+1}=u_n+h[-x_nu_n-y_n]$

where represents the step size.

Let

$\\h=0.1 \\y_0=2 \\u_0=3$

Substitute these values into the previous formulas and continue in this fashion until the approximation for y(0.2) is found.

$\\y_1=y_0+(0.1)u_0=2+(0.1)(3)=2.3 \\u_1=u_0+(0.1)[-x_0u_0-y_0]=3+(0.1)[0(2)-2]=2.8 \\y_2=y_1+(0.1)u_1=2.3+(0.1)(2.8)=2.58 \\u_2=u_1+(0.1)[-x_1u_1-y_1]=2.8+(0.1)[-0.1(2.8)-2.3]=2.542$

Therefore,

$y(0.2)\approx2.58$

Report an Error

Example Question #1 : Euler Method

Use the implicit Euler method to approximate y(3) for y' = 5y , given that y(0) = 4 , using a time step of h = 1.

Possible Answers:

$\frac{1}{32}$

$\frac{1}{16}$

$-\frac{1}{16}$

Correct answer:

$-\frac{1}{16}$

Explanation:

In the implicit method, the amount to increase is given by $h \cdot f(t_{i+1}, y_{i+1})$ , or in this case $\mu_i = \mu_{i-1}+ 1 \cdot (5\mu_i)$ . Note, you can't just plug in to this form of the equation, because it's implicit: $\mu_i$ is on both sides. Thankfully, this is an easy enough form that you can solve explicitly. Otherwise, you would have to use an approximation method like newton's method to find $\mu_i$ . Solving explicitly, we have $-4\mu_i = \mu_{i-1}$ and $\mu_i = -\frac{\mu_{i-1}}{4}$ .

Thus, $y(1) \approx \mu_1 = -\frac{4}{4} = -1$

$y(2) \approx \mu_2 = -\frac{-1}{4} = \frac{1}{4}$

$y(3) \approx \mu_3 = -\frac{\frac{1}{4}}{4} = -\frac{1}{16}$

Thus, we have a final answer of $-\frac{1}{16}$

Report an Error

Example Question #2 : Euler Method

Use two steps of Euler's Method with h=0.1 on

$y' = x\sqrt{y} \ \ \ y(1) = 4$

To three decimal places

Possible Answers:

4.420

4.413

4.428

4.408

4.425

Correct answer:

4.425

Explanation:

Euler's Method gives us

$y_{n+1} = y_n + hf(x_n,y_n) = y_n + (0.1)x_n\sqrt{y_n}$

Taking one step

$y_1 = y_0 + (0.1)x_0\sqrt{y_0} = 4 + (0.1)(1)\sqrt{4} = 4.2$

Taking another step

$y_2 = y_1 + (0.1)x_1\sqrt{y_1} = 4.2 + (0.1)(1.1)\sqrt{4.2} \approx 4.425$

Report an Error

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

The two-step Adams-Bashforth method of approximation uses the approximation scheme $y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ .

Given that 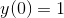y(0) = 1 and y(1) = 2 , use the Adams-Bashforth method to approximate y(3) for y = -y^2 with a step size of h = 1.

Possible Answers:

$\frac{33}{4}$

$\frac{97}{8}$

$\frac{133}{8}$

$\frac{55}{8}$

$-\frac{159}{8}$

Correct answer:

$-\frac{159}{8}$

Explanation:

In this problem, we're given two points, so we can start plugging in immediately. If we were not, we could approximate $y_{i+1}$ by using the explicit Euler method on $y_{i}$ .

Plugging into 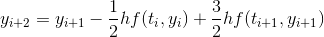$y_{i+2} = y_{i+1} - \frac{1}{2}hf(t_i, y_i) + \frac{3}{2}hf(t_{i+1}, y_{i+1})$ , we have

$y(2) \approx \mu_2 = 2 -\frac{1}{2}\cdot 1 \cdot -1^2 + \frac{3}{2}\cdot 1 \cdot -2^2 = 2 +\frac{1}{2} - 6 = -\frac{7}{2}$

$y(3)\approx \mu_3 = -\frac{7}{2} + \frac{1}{2}\cdot4 - \frac{3}{2}\cdot \frac{49}{4} =-\frac{159}{8}$ .

Note, our approximation likely won't be very good with such large a time step, but the process doesn't change regardless of the accuracy.

$y(3)\approx -\frac{159}{8}$

Report an Error

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Find the solutions to the second order boundary-value problem. y'' -2y' + 2y = 0 , y(0) = 0 , $y\left(\frac{\pi}{2}\right) = 1$ .

Possible Answers:

There are no solutions to the boundary value problem.

$y = 10e^{2t}\sin(2t)$

$y = 5e^t\sin(t) + 3e^t\cos(t)$

$y = e^{t}\sin(t) - e^t\cos(t)$

$y = e^{t -\frac{\pi}{2}}\sin(t)$

Correct answer:

$y = e^{t -\frac{\pi}{2}}\sin(t)$

Explanation:

The characteristic equation of y'' -2y' + 2y = 0 is $\lambda^2 - 2\lambda + 2 = 0$ , with solutions of $\frac{2 \pm \sqrt{4 - 8}}{2} = 1 \pm i$ . Thus, the general solution to the homogeneous problem is $y = c_1e^t\sin(t) + c_2e^t\cos(t)$ . Plugging in our conditions, we find that y(0) = c_2 = 0 , so that $y = c_1e^t\sin(t)$ . Plugging in our second condition, we find that $y\left(\frac{\pi}{2}\right) = c_1e^{\frac{\pi}{2}} = 1$ and that $c_1 = e^{-\frac{\pi}{2}}$ .

Thus, the final solution is $y = e^{t -\frac{\pi}{2}}\sin(t)$ .

Report an Error

Example Question #2 : Numerical Solutions Of Ordinary Differential Equations

Find the solutions to the second order boundary-value problem. y'' + 9y = 0 , y(0) = 0 , $y\left(2\pi\right) = 1$ .

Possible Answers:

$y = \sin(3t) + 2 \cos(3t)$

$y = 3\sin(3t)$

$y = 3\cos(3t)$

There are no solutions to the boundary value problem.

$y = 4\sin(3t) - \cos(3t)$

Correct answer:

There are no solutions to the boundary value problem.

Explanation:

The characteristic equation of y'' + 9y = 0 is $\lambda^2 + 9 = 0$ with solutions of $\pm 3i$ . This tells us that the solution to the homogeneous equation is $y = c_1\sin(3t) + c_2\cos(3t)$ . Plugging in our conditions, we find that y(0) = c_2 = 0 so that $y = c_1\sin(3t)$ . Plugging in our second condition, we have $y(2\pi) = 0 = 1$ which is obviously false.

This problem demonstrates the important distinction between initial value problems and boundary value problems: Boundary value problems don't always have solutions. This is one such case, as we can't find c_1, c_2 that satisfy our conditions.

Report an Error

View Differential Equations Tutors

Pankaj
Certified Tutor

University of Delhi, Electrical Engineer, Electrical Engineering. Columbia University in the City of New York, Master of Arts...

View Differential Equations Tutors

Robert Edward
Certified Tutor

University of Calgary, Master of Engineering, Chemistry. University of Ottawa, Bachelor of Engineering, Civil Engineering.

View Differential Equations Tutors

Scott
Certified Tutor

Florida State University, Bachelor of Science, Applied Mathematics. Florida State University, Bachelor of Science, Astrophysi...

All Differential Equations Resources

1 Diagnostic Test 29 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Philadelphia, Calculus Tutors in San Francisco-Bay Area, Spanish Tutors in Phoenix, SSAT Tutors in Seattle, Spanish Tutors in Chicago, Computer Science Tutors in Houston, Spanish Tutors in Houston, French Tutors in Dallas Fort Worth, SAT Tutors in Washington DC, MCAT Tutors in New York City

Popular Courses & Classes

ISEE Courses & Classes in Chicago, SAT Courses & Classes in Washington DC, MCAT Courses & Classes in Philadelphia, Spanish Courses & Classes in New York City, ACT Courses & Classes in San Francisco-Bay Area, ISEE Courses & Classes in Philadelphia, ACT Courses & Classes in Seattle, SSAT Courses & Classes in Seattle, SAT Courses & Classes in Boston, MCAT Courses & Classes in Boston

Popular Test Prep

LSAT Test Prep in Houston, SAT Test Prep in Houston, SAT Test Prep in Phoenix, LSAT Test Prep in Chicago, MCAT Test Prep in Seattle, LSAT Test Prep in Los Angeles, GMAT Test Prep in Chicago, SAT Test Prep in Seattle, ACT Test Prep in San Francisco-Bay Area, ISEE Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Differential Equations : Numerical Solutions of Ordinary Differential Equations

Study concepts, example questions & explanations for Differential Equations

All Differential Equations Resources

Example Questions

Example Question #1 : Euler Method

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Example Question #1 : Euler Method

Example Question #2 : Euler Method

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Example Question #1 : Numerical Solutions Of Ordinary Differential Equations

Example Question #2 : Numerical Solutions Of Ordinary Differential Equations

All Differential Equations Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: